注意
点击此处下载完整的示例代码
DCGAN 教程¶
创建日期:2018 年 7 月 31 日 | 最后更新:2024 年 1 月 19 日 | 最后验证:2024 年 11 月 5 日
作者: Nathan Inkawhich
引言¶
本教程将通过一个示例介绍 DCGAN。我们将训练一个生成对抗网络 (GAN),在展示了许多真实名人照片后,使其生成新的名人照片。这里的绝大多数代码都来自 pytorch/examples 中的 DCGAN 实现,本文档将详细解释实现过程,并阐明该模型的工作原理和原因。但请放心,无需 GAN 的先验知识,不过初学者可能需要花一些时间思考其底层实际发生的事情。此外,为了节省时间,有一两个 GPU 会很有帮助。让我们从头开始。
生成对抗网络¶
什么是 GAN?¶
GAN 是一种框架,用于教导深度学习模型捕捉训练数据分布,以便我们可以从该相同分布中生成新数据。GAN 由 Ian Goodfellow 于 2014 年发明,并首次在论文 Generative Adversarial Nets 中描述。它们由两个不同的模型组成:一个*生成器*(generator) 和一个*判别器*(discriminator)。生成器的任务是生成看起来像训练图像的“伪造”图像。判别器的任务是查看一张图像并输出它是否是真实的训练图像或来自生成器的伪造图像。在训练过程中,生成器不断尝试通过生成越来越好的伪造品来胜过判别器,而判别器则致力于成为更好的侦探,正确分类真实图像和伪造图像。这场博弈的均衡点是生成器生成看起来像是直接来自训练数据的完美伪造品,而判别器则总是以 50% 的置信度猜测生成器的输出是真实还是伪造的。
现在,让我们定义一些将在整个教程中使用的符号,首先是判别器。令 \(x\) 表示图像数据。 \(D(x)\) 是判别器网络,它输出 \(x\) 来自训练数据而非生成器的(标量)概率。在这里,由于我们处理的是图像,\(D(x)\) 的输入是 CHW 大小为 3x64x64 的图像。直观上,当 \(x\) 来自训练数据时,\(D(x)\) 应该很高;当 \(x\) 来自生成器时,\(D(x)\) 应该很低。 \(D(x)\) 也可以被视为传统的二分类器。
对于生成器的符号,令 \(z\) 为从标准正态分布中采样的潜在空间向量。 \(G(z)\) 表示生成器函数,它将潜在向量 \(z\) 映射到数据空间。 \(G\) 的目标是估计训练数据来源的分布 (\(p_{data}\)),以便它可以从该估计分布 (\(p_g\)) 中生成伪造样本。
因此, \(D(G(z))\) 是生成器 \(G\) 的输出是真实图像的概率(标量)。如 Goodfellow 的论文中所述,\(D\) 和 \(G\) 进行一场最小最大博弈,其中 \(D\) 试图最大化其正确分类真实和伪造样本的概率 (\(logD(x)\)),而 \(G\) 试图最小化 \(D\) 将其输出预测为伪造的概率 (\(log(1-D(G(z)))\))。根据论文,GAN 的损失函数是
理论上,这场最小最大博弈的解是 \(p_g = p_{data}\),判别器随机猜测输入是真实还是伪造的。然而,GAN 的收敛理论仍在积极研究中,在现实中模型并不总是训练到这一点。
什么是 DCGAN?¶
DCGAN 是上述 GAN 的直接扩展,不同之处在于它在判别器和生成器中分别明确使用了卷积层和转置卷积层。它最初由 Radford 等人在论文 Unsupervised Representation Learning With Deep Convolutional Generative Adversarial Networks 中描述。判别器由带步长的 卷积层、批标准化层和 LeakyReLU 激活函数组成。输入是 3x64x64 的输入图像,输出是输入来自真实数据分布的标量概率。生成器由 转置卷积层、批标准化层和 ReLU 激活函数组成。输入是潜在向量 \(z\),该向量从标准正态分布中抽取,输出是 3x64x64 的 RGB 图像。带步长的转置卷积层允许将潜在向量转换为与图像具有相同形状的体积。在论文中,作者还给出了一些关于如何设置优化器、如何计算损失函数以及如何初始化模型权重的技巧,所有这些将在接下来的部分中解释。
#%matplotlib inline
import argparse
import os
import random
import torch
import torch.nn as nn
import torch.nn.parallel
import torch.optim as optim
import torch.utils.data
import torchvision.datasets as dset
import torchvision.transforms as transforms
import torchvision.utils as vutils
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from IPython.display import HTML
# Set random seed for reproducibility
manualSeed = 999
#manualSeed = random.randint(1, 10000) # use if you want new results
print("Random Seed: ", manualSeed)
random.seed(manualSeed)
torch.manual_seed(manualSeed)
torch.use_deterministic_algorithms(True) # Needed for reproducible results
Random Seed: 999
输入参数¶
让我们为运行定义一些输入参数
dataroot- 数据集文件夹根目录的路径。我们将在下一节详细讨论数据集。workers- 使用DataLoader加载数据的工作线程数量。batch_size- 训练中使用的批次大小。DCGAN 论文使用 128 的批次大小。image_size- 用于训练的图像的空间尺寸。本实现默认为 64x64。如果需要其他尺寸,必须更改 D 和 G 的结构。更多详情请参见此处。nc- 输入图像中的颜色通道数量。对于彩色图像,此值为 3。nz- 潜在向量的长度。ngf- 与通过生成器传播的特征图深度有关。ndf- 设置通过判别器传播的特征图深度。num_epochs- 要运行的训练轮次数量。训练时间越长可能导致结果越好,但也会花费更长时间。lr- 训练的学习率。如 DCGAN 论文所述,此值应为 0.0002。beta1- Adam 优化器的 beta1 超参数。如论文所述,此值应为 0.5。ngpu- 可用 GPU 数量。如果此值为 0,代码将在 CPU 模式下运行。如果此值大于 0,将在相应数量的 GPU 上运行。
# Root directory for dataset
dataroot = "data/celeba"
# Number of workers for dataloader
workers = 2
# Batch size during training
batch_size = 128
# Spatial size of training images. All images will be resized to this
# size using a transformer.
image_size = 64
# Number of channels in the training images. For color images this is 3
nc = 3
# Size of z latent vector (i.e. size of generator input)
nz = 100
# Size of feature maps in generator
ngf = 64
# Size of feature maps in discriminator
ndf = 64
# Number of training epochs
num_epochs = 5
# Learning rate for optimizers
lr = 0.0002
# Beta1 hyperparameter for Adam optimizers
beta1 = 0.5
# Number of GPUs available. Use 0 for CPU mode.
ngpu = 1
数据¶
在本教程中,我们将使用 Celeb-A 人脸数据集,可以在链接的网站下载,或在 Google Drive 下载。数据集将下载为一个名为 img_align_celeba.zip 的文件。下载后,创建一个名为 celeba 的目录,并将 zip 文件解压到该目录中。然后,将本 notebook 的 dataroot 输入设置为您刚刚创建的 celeba 目录。结果目录结构应为
/path/to/celeba
-> img_align_celeba
-> 188242.jpg
-> 173822.jpg
-> 284702.jpg
-> 537394.jpg
...
这是重要的一步,因为我们将使用 ImageFolder 数据集类,该类要求数据集根目录中必须有子目录。现在,我们可以创建数据集,创建数据加载器,设置运行设备,最后可视化一些训练数据。
# We can use an image folder dataset the way we have it setup.
# Create the dataset
dataset = dset.ImageFolder(root=dataroot,
transform=transforms.Compose([
transforms.Resize(image_size),
transforms.CenterCrop(image_size),
transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5)),
]))
# Create the dataloader
dataloader = torch.utils.data.DataLoader(dataset, batch_size=batch_size,
shuffle=True, num_workers=workers)
# Decide which device we want to run on
device = torch.device("cuda:0" if (torch.cuda.is_available() and ngpu > 0) else "cpu")
# Plot some training images
real_batch = next(iter(dataloader))
plt.figure(figsize=(8,8))
plt.axis("off")
plt.title("Training Images")
plt.imshow(np.transpose(vutils.make_grid(real_batch[0].to(device)[:64], padding=2, normalize=True).cpu(),(1,2,0)))
plt.show()

实现¶
设置好输入参数并准备好数据集后,我们现在可以进入实现环节。我们将从权重初始化策略开始,然后详细讨论生成器、判别器、损失函数和训练循环。
权重初始化¶
根据 DCGAN 论文,作者指定所有模型权重应从均值 mean=0、标准差 stdev=0.02 的正态分布中随机初始化。weights_init 函数接受一个已初始化的模型作为输入,并重新初始化所有卷积层、转置卷积层和批标准化层以满足此标准。此函数在模型初始化后立即应用于模型。
# custom weights initialization called on ``netG`` and ``netD``
def weights_init(m):
classname = m.__class__.__name__
if classname.find('Conv') != -1:
nn.init.normal_(m.weight.data, 0.0, 0.02)
elif classname.find('BatchNorm') != -1:
nn.init.normal_(m.weight.data, 1.0, 0.02)
nn.init.constant_(m.bias.data, 0)
生成器¶
生成器 \(G\) 旨在将潜在空间向量 (\(z\)) 映射到数据空间。由于我们的数据是图像,将 \(z\) 转换为数据空间最终意味着创建一个与训练图像具有相同尺寸 (即 3x64x64) 的 RGB 图像。在实践中,这通过一系列带步长的二维转置卷积层来实现,每个层都与一个二维批标准化层和一个 relu 激活函数配对。生成器的输出通过 tanh 函数馈送,将其返回到 \([-1,1]\) 的输入数据范围。值得注意的是,转置卷积层之后存在批标准化函数,这是 DCGAN 论文的关键贡献之一。这些层有助于训练期间的梯度流。DCGAN 论文中的生成器图像如下所示。
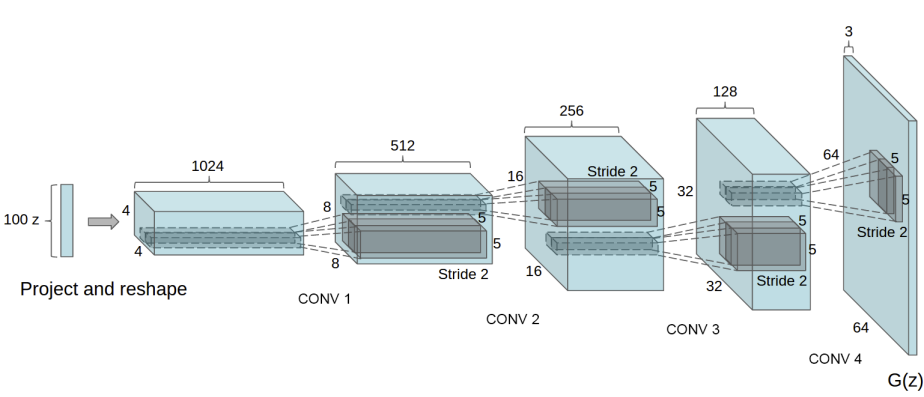
请注意,我们在输入参数部分设置的输入 (nz、ngf 和 nc) 如何影响代码中的生成器架构。nz 是 z 输入向量的长度,ngf 与通过生成器传播的特征图大小有关,nc 是输出图像中的通道数(对于 RGB 图像设置为 3)。下面是生成器的代码。
# Generator Code
class Generator(nn.Module):
def __init__(self, ngpu):
super(Generator, self).__init__()
self.ngpu = ngpu
self.main = nn.Sequential(
# input is Z, going into a convolution
nn.ConvTranspose2d( nz, ngf * 8, 4, 1, 0, bias=False),
nn.BatchNorm2d(ngf * 8),
nn.ReLU(True),
# state size. ``(ngf*8) x 4 x 4``
nn.ConvTranspose2d(ngf * 8, ngf * 4, 4, 2, 1, bias=False),
nn.BatchNorm2d(ngf * 4),
nn.ReLU(True),
# state size. ``(ngf*4) x 8 x 8``
nn.ConvTranspose2d( ngf * 4, ngf * 2, 4, 2, 1, bias=False),
nn.BatchNorm2d(ngf * 2),
nn.ReLU(True),
# state size. ``(ngf*2) x 16 x 16``
nn.ConvTranspose2d( ngf * 2, ngf, 4, 2, 1, bias=False),
nn.BatchNorm2d(ngf),
nn.ReLU(True),
# state size. ``(ngf) x 32 x 32``
nn.ConvTranspose2d( ngf, nc, 4, 2, 1, bias=False),
nn.Tanh()
# state size. ``(nc) x 64 x 64``
)
def forward(self, input):
return self.main(input)
现在,我们可以实例化生成器并应用 weights_init 函数。查看打印出的模型,了解生成器对象的结构。
# Create the generator
netG = Generator(ngpu).to(device)
# Handle multi-GPU if desired
if (device.type == 'cuda') and (ngpu > 1):
netG = nn.DataParallel(netG, list(range(ngpu)))
# Apply the ``weights_init`` function to randomly initialize all weights
# to ``mean=0``, ``stdev=0.02``.
netG.apply(weights_init)
# Print the model
print(netG)
Generator(
(main): Sequential(
(0): ConvTranspose2d(100, 512, kernel_size=(4, 4), stride=(1, 1), bias=False)
(1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(2): ReLU(inplace=True)
(3): ConvTranspose2d(512, 256, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
(4): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(5): ReLU(inplace=True)
(6): ConvTranspose2d(256, 128, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
(7): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(8): ReLU(inplace=True)
(9): ConvTranspose2d(128, 64, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
(10): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(11): ReLU(inplace=True)
(12): ConvTranspose2d(64, 3, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
(13): Tanh()
)
)
判别器¶
如前所述,判别器 \(D\) 是一个二分类网络,它将图像作为输入,并输出输入图像是真实图像(而不是伪造图像)的标量概率。在这里,\(D\) 接收一个 3x64x64 的输入图像,通过一系列 Conv2d、BatchNorm2d 和 LeakyReLU 层进行处理,并通过 Sigmoid 激活函数输出最终概率。如果问题需要,此架构可以扩展更多层,但使用带步长的卷积、批标准化和 LeakyReLU 具有重要意义。DCGAN 论文提到,使用带步长的卷积而不是池化进行下采样是一个好做法,因为它让网络学习自己的池化函数。此外,批标准化和 LeakyReLU 函数促进了健康的梯度流,这对于 \(G\) 和 \(D\) 的学习过程至关重要。
判别器代码
class Discriminator(nn.Module):
def __init__(self, ngpu):
super(Discriminator, self).__init__()
self.ngpu = ngpu
self.main = nn.Sequential(
# input is ``(nc) x 64 x 64``
nn.Conv2d(nc, ndf, 4, 2, 1, bias=False),
nn.LeakyReLU(0.2, inplace=True),
# state size. ``(ndf) x 32 x 32``
nn.Conv2d(ndf, ndf * 2, 4, 2, 1, bias=False),
nn.BatchNorm2d(ndf * 2),
nn.LeakyReLU(0.2, inplace=True),
# state size. ``(ndf*2) x 16 x 16``
nn.Conv2d(ndf * 2, ndf * 4, 4, 2, 1, bias=False),
nn.BatchNorm2d(ndf * 4),
nn.LeakyReLU(0.2, inplace=True),
# state size. ``(ndf*4) x 8 x 8``
nn.Conv2d(ndf * 4, ndf * 8, 4, 2, 1, bias=False),
nn.BatchNorm2d(ndf * 8),
nn.LeakyReLU(0.2, inplace=True),
# state size. ``(ndf*8) x 4 x 4``
nn.Conv2d(ndf * 8, 1, 4, 1, 0, bias=False),
nn.Sigmoid()
)
def forward(self, input):
return self.main(input)
现在,与生成器一样,我们可以创建判别器,应用 weights_init 函数,并打印模型的结构。
# Create the Discriminator
netD = Discriminator(ngpu).to(device)
# Handle multi-GPU if desired
if (device.type == 'cuda') and (ngpu > 1):
netD = nn.DataParallel(netD, list(range(ngpu)))
# Apply the ``weights_init`` function to randomly initialize all weights
# like this: ``to mean=0, stdev=0.2``.
netD.apply(weights_init)
# Print the model
print(netD)
Discriminator(
(main): Sequential(
(0): Conv2d(3, 64, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
(1): LeakyReLU(negative_slope=0.2, inplace=True)
(2): Conv2d(64, 128, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
(3): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(4): LeakyReLU(negative_slope=0.2, inplace=True)
(5): Conv2d(128, 256, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
(6): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(7): LeakyReLU(negative_slope=0.2, inplace=True)
(8): Conv2d(256, 512, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
(9): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(10): LeakyReLU(negative_slope=0.2, inplace=True)
(11): Conv2d(512, 1, kernel_size=(4, 4), stride=(1, 1), bias=False)
(12): Sigmoid()
)
)
损失函数和优化器¶
设置好 \(D\) 和 \(G\) 后,我们可以通过损失函数和优化器指定它们的学习方式。我们将使用二元交叉熵损失 (BCELoss) 函数,该函数在 PyTorch 中定义为
请注意,此函数提供了目标函数中两个对数分量(即 \(log(D(x))\) 和 \(log(1-D(G(z)))\))的计算。我们可以通过 \(y\) 输入指定使用 BCE 方程的哪个部分。这将在即将到来的训练循环中实现,但重要的是要理解我们如何只需更改 \(y\)(即真实标签)即可选择我们希望计算哪个分量。
接下来,我们将真实标签定义为 1,将伪造标签定义为 0。这些标签将在计算 \(D\) 和 \(G\) 的损失时使用,这也是原始 GAN 论文中使用的约定。最后,我们设置了两个独立的优化器,一个用于 \(D\),一个用于 \(G\)。如 DCGAN 论文所述,两者都是 Adam 优化器,学习率为 0.0002,Beta1 = 0.5。为了跟踪生成器的学习进展,我们将生成一个固定的批次潜在向量,这些向量从高斯分布中抽取(即 fixed_noise)。在训练循环中,我们将定期将此 fixed_noise 输入到 \(G\) 中,并在迭代过程中看到图像从噪声中形成。
# Initialize the ``BCELoss`` function
criterion = nn.BCELoss()
# Create batch of latent vectors that we will use to visualize
# the progression of the generator
fixed_noise = torch.randn(64, nz, 1, 1, device=device)
# Establish convention for real and fake labels during training
real_label = 1.
fake_label = 0.
# Setup Adam optimizers for both G and D
optimizerD = optim.Adam(netD.parameters(), lr=lr, betas=(beta1, 0.999))
optimizerG = optim.Adam(netG.parameters(), lr=lr, betas=(beta1, 0.999))
训练¶
最后,既然我们已经定义了 GAN 框架的所有组成部分,我们就可以训练它了。请注意,训练 GAN 在某种程度上是一门艺术,因为不正确的超参数设置会导致模式崩溃,且很难解释哪里出了问题。在这里,我们将密切遵循 Goodfellow 的论文中的算法 1,同时遵守 ganhacks 中展示的一些最佳实践。具体来说,我们将“为真实和伪造图像构建不同的小批量”,并调整 G 的目标函数以最大化 \(log(D(G(z)))\)。训练分为两个主要部分。第一部分更新判别器,第二部分更新生成器。
第一部分 - 训练判别器
回顾一下,训练判别器的目标是最大化正确分类给定输入是真实还是伪造的概率。用 Goodfellow 的话说,我们希望“通过提升其随机梯度来更新判别器”。实际上,我们希望最大化 \(log(D(x)) + log(1-D(G(z)))\)。由于 ganhacks 中建议使用独立的小批量,我们将分两步计算它。首先,我们将从训练集中构建一个真实样本的批次,通过 \(D\) 进行前向传播,计算损失 (\(log(D(x))\)),然后在反向传播中计算梯度。其次,我们将使用当前的生成器构建一个伪造样本的批次,通过 \(D\) 对此批次进行前向传播,计算损失 (\(log(1-D(G(z)))\)),并通过反向传播*累积*梯度。现在,在累积了来自所有真实批次和所有伪造批次的梯度后,我们调用判别器优化器的一个步长。
第二部分 - 训练生成器
如原始论文所述,我们希望通过最小化 \(log(1-D(G(z)))\) 来训练生成器,以努力生成更好的伪造品。如前所述,Goodfellow 表明这种方式无法提供足够的梯度,特别是在学习过程的早期。作为修正,我们转而希望最大化 \(log(D(G(z)))\)。在代码中,我们通过以下方式实现这一点:使用判别器对第一部分中的生成器输出进行分类,*使用真实标签作为真实值*计算 G 的损失,在反向传播中计算 G 的梯度,最后使用优化器步长更新 G 的参数。使用真实标签作为损失函数的真实值可能看起来有悖常理,但这允许我们使用 BCELoss 中的 \(log(x)\) 部分(而不是 \(log(1-x)\) 部分),这正是我们想要的。
最后,我们将进行一些统计报告,并在每个轮次结束时将我们的 fixed_noise 批次通过生成器,以便直观地跟踪 G 训练的进展。报告的训练统计信息如下
Loss_D - 判别器损失,计算为所有真实和所有伪造批次损失的总和 (\(log(D(x)) + log(1 - D(G(z)))\))。
Loss_G - 生成器损失,计算为 \(log(D(G(z)))\)
D(x) - 判别器对所有真实样本批次的平均输出(跨批次)。这个值理论上应该从接近 1 开始,然后随着生成器 (G) 的改进而收敛到 0.5。思考一下这是为什么。
D(G(z)) - 判别器对所有生成(假)样本批次的平均输出。第一个数字是判别器 (D) 更新之前的值,第二个数字是 D 更新之后的值。这些数字应该从接近 0 开始,然后随着 G 的改进而收敛到 0.5。思考一下这是为什么。
注意:这一步可能需要一段时间,具体取决于你运行的 epoch 数量以及你是否从数据集中移除了部分数据。
# Training Loop
# Lists to keep track of progress
img_list = []
G_losses = []
D_losses = []
iters = 0
print("Starting Training Loop...")
# For each epoch
for epoch in range(num_epochs):
# For each batch in the dataloader
for i, data in enumerate(dataloader, 0):
############################
# (1) Update D network: maximize log(D(x)) + log(1 - D(G(z)))
###########################
## Train with all-real batch
netD.zero_grad()
# Format batch
real_cpu = data[0].to(device)
b_size = real_cpu.size(0)
label = torch.full((b_size,), real_label, dtype=torch.float, device=device)
# Forward pass real batch through D
output = netD(real_cpu).view(-1)
# Calculate loss on all-real batch
errD_real = criterion(output, label)
# Calculate gradients for D in backward pass
errD_real.backward()
D_x = output.mean().item()
## Train with all-fake batch
# Generate batch of latent vectors
noise = torch.randn(b_size, nz, 1, 1, device=device)
# Generate fake image batch with G
fake = netG(noise)
label.fill_(fake_label)
# Classify all fake batch with D
output = netD(fake.detach()).view(-1)
# Calculate D's loss on the all-fake batch
errD_fake = criterion(output, label)
# Calculate the gradients for this batch, accumulated (summed) with previous gradients
errD_fake.backward()
D_G_z1 = output.mean().item()
# Compute error of D as sum over the fake and the real batches
errD = errD_real + errD_fake
# Update D
optimizerD.step()
############################
# (2) Update G network: maximize log(D(G(z)))
###########################
netG.zero_grad()
label.fill_(real_label) # fake labels are real for generator cost
# Since we just updated D, perform another forward pass of all-fake batch through D
output = netD(fake).view(-1)
# Calculate G's loss based on this output
errG = criterion(output, label)
# Calculate gradients for G
errG.backward()
D_G_z2 = output.mean().item()
# Update G
optimizerG.step()
# Output training stats
if i % 50 == 0:
print('[%d/%d][%d/%d]\tLoss_D: %.4f\tLoss_G: %.4f\tD(x): %.4f\tD(G(z)): %.4f / %.4f'
% (epoch, num_epochs, i, len(dataloader),
errD.item(), errG.item(), D_x, D_G_z1, D_G_z2))
# Save Losses for plotting later
G_losses.append(errG.item())
D_losses.append(errD.item())
# Check how the generator is doing by saving G's output on fixed_noise
if (iters % 500 == 0) or ((epoch == num_epochs-1) and (i == len(dataloader)-1)):
with torch.no_grad():
fake = netG(fixed_noise).detach().cpu()
img_list.append(vutils.make_grid(fake, padding=2, normalize=True))
iters += 1
Starting Training Loop...
[0/5][0/1583] Loss_D: 1.4640 Loss_G: 6.9366 D(x): 0.7143 D(G(z)): 0.5877 / 0.0017
[0/5][50/1583] Loss_D: 1.3473 Loss_G: 26.0342 D(x): 0.9521 D(G(z)): 0.6274 / 0.0000
[0/5][100/1583] Loss_D: 0.4592 Loss_G: 5.4997 D(x): 0.8385 D(G(z)): 0.1582 / 0.0096
[0/5][150/1583] Loss_D: 0.4003 Loss_G: 4.9369 D(x): 0.9549 D(G(z)): 0.2696 / 0.0112
[0/5][200/1583] Loss_D: 1.0697 Loss_G: 7.1552 D(x): 0.9390 D(G(z)): 0.5277 / 0.0016
[0/5][250/1583] Loss_D: 0.2654 Loss_G: 3.7994 D(x): 0.8486 D(G(z)): 0.0386 / 0.0498
[0/5][300/1583] Loss_D: 0.8607 Loss_G: 1.7948 D(x): 0.5738 D(G(z)): 0.0922 / 0.2307
[0/5][350/1583] Loss_D: 0.4578 Loss_G: 3.7834 D(x): 0.8936 D(G(z)): 0.2463 / 0.0383
[0/5][400/1583] Loss_D: 0.4972 Loss_G: 5.1323 D(x): 0.9523 D(G(z)): 0.3053 / 0.0126
[0/5][450/1583] Loss_D: 1.3933 Loss_G: 1.9958 D(x): 0.4034 D(G(z)): 0.0379 / 0.1982
[0/5][500/1583] Loss_D: 0.9834 Loss_G: 2.8194 D(x): 0.5936 D(G(z)): 0.1847 / 0.1077
[0/5][550/1583] Loss_D: 0.5884 Loss_G: 7.6739 D(x): 0.8827 D(G(z)): 0.3119 / 0.0013
[0/5][600/1583] Loss_D: 0.5217 Loss_G: 5.6103 D(x): 0.9342 D(G(z)): 0.3160 / 0.0085
[0/5][650/1583] Loss_D: 0.4254 Loss_G: 3.8598 D(x): 0.8154 D(G(z)): 0.1438 / 0.0317
[0/5][700/1583] Loss_D: 0.3483 Loss_G: 4.2089 D(x): 0.7952 D(G(z)): 0.0355 / 0.0240
[0/5][750/1583] Loss_D: 0.5566 Loss_G: 6.2280 D(x): 0.9148 D(G(z)): 0.3040 / 0.0042
[0/5][800/1583] Loss_D: 0.2617 Loss_G: 5.5604 D(x): 0.8322 D(G(z)): 0.0383 / 0.0080
[0/5][850/1583] Loss_D: 1.6397 Loss_G: 10.7162 D(x): 0.9620 D(G(z)): 0.6981 / 0.0002
[0/5][900/1583] Loss_D: 1.0194 Loss_G: 5.4787 D(x): 0.8427 D(G(z)): 0.4678 / 0.0094
[0/5][950/1583] Loss_D: 0.4182 Loss_G: 4.7106 D(x): 0.8578 D(G(z)): 0.1802 / 0.0222
[0/5][1000/1583] Loss_D: 0.4757 Loss_G: 3.8595 D(x): 0.8051 D(G(z)): 0.1514 / 0.0416
[0/5][1050/1583] Loss_D: 0.6044 Loss_G: 2.9149 D(x): 0.7372 D(G(z)): 0.1696 / 0.0809
[0/5][1100/1583] Loss_D: 0.7655 Loss_G: 2.3512 D(x): 0.6174 D(G(z)): 0.0593 / 0.1484
[0/5][1150/1583] Loss_D: 0.7374 Loss_G: 3.1968 D(x): 0.6097 D(G(z)): 0.0709 / 0.0777
[0/5][1200/1583] Loss_D: 0.6484 Loss_G: 4.1837 D(x): 0.8723 D(G(z)): 0.3046 / 0.0323
[0/5][1250/1583] Loss_D: 0.6404 Loss_G: 4.9987 D(x): 0.8959 D(G(z)): 0.3395 / 0.0124
[0/5][1300/1583] Loss_D: 0.7700 Loss_G: 7.7520 D(x): 0.9699 D(G(z)): 0.4454 / 0.0011
[0/5][1350/1583] Loss_D: 0.4115 Loss_G: 3.8996 D(x): 0.8038 D(G(z)): 0.1153 / 0.0301
[0/5][1400/1583] Loss_D: 0.5865 Loss_G: 3.3128 D(x): 0.8186 D(G(z)): 0.2586 / 0.0521
[0/5][1450/1583] Loss_D: 0.7625 Loss_G: 2.5499 D(x): 0.6857 D(G(z)): 0.2169 / 0.1131
[0/5][1500/1583] Loss_D: 1.3006 Loss_G: 3.9234 D(x): 0.4019 D(G(z)): 0.0053 / 0.0425
[0/5][1550/1583] Loss_D: 1.0234 Loss_G: 2.1976 D(x): 0.4556 D(G(z)): 0.0291 / 0.1659
[1/5][0/1583] Loss_D: 0.3606 Loss_G: 3.7421 D(x): 0.8785 D(G(z)): 0.1770 / 0.0377
[1/5][50/1583] Loss_D: 0.6186 Loss_G: 2.6328 D(x): 0.6461 D(G(z)): 0.0559 / 0.1141
[1/5][100/1583] Loss_D: 0.6551 Loss_G: 3.9456 D(x): 0.6392 D(G(z)): 0.0641 / 0.0429
[1/5][150/1583] Loss_D: 0.7882 Loss_G: 6.6105 D(x): 0.9553 D(G(z)): 0.4592 / 0.0031
[1/5][200/1583] Loss_D: 0.5069 Loss_G: 2.1326 D(x): 0.7197 D(G(z)): 0.0957 / 0.1621
[1/5][250/1583] Loss_D: 0.4229 Loss_G: 2.8329 D(x): 0.7680 D(G(z)): 0.0920 / 0.0915
[1/5][300/1583] Loss_D: 0.3388 Loss_G: 3.2621 D(x): 0.8501 D(G(z)): 0.1096 / 0.0758
[1/5][350/1583] Loss_D: 0.2864 Loss_G: 4.5487 D(x): 0.9182 D(G(z)): 0.1608 / 0.0184
[1/5][400/1583] Loss_D: 0.3158 Loss_G: 3.3892 D(x): 0.8432 D(G(z)): 0.1100 / 0.0554
[1/5][450/1583] Loss_D: 1.2332 Loss_G: 8.1937 D(x): 0.9940 D(G(z)): 0.6184 / 0.0008
[1/5][500/1583] Loss_D: 0.4001 Loss_G: 3.4084 D(x): 0.8584 D(G(z)): 0.1890 / 0.0472
[1/5][550/1583] Loss_D: 1.5110 Loss_G: 2.5652 D(x): 0.3283 D(G(z)): 0.0121 / 0.1440
[1/5][600/1583] Loss_D: 0.5324 Loss_G: 2.1393 D(x): 0.6765 D(G(z)): 0.0592 / 0.1596
[1/5][650/1583] Loss_D: 0.5493 Loss_G: 1.9572 D(x): 0.6725 D(G(z)): 0.0439 / 0.1998
[1/5][700/1583] Loss_D: 0.6842 Loss_G: 3.5358 D(x): 0.7578 D(G(z)): 0.2744 / 0.0450
[1/5][750/1583] Loss_D: 1.5829 Loss_G: 0.7034 D(x): 0.3024 D(G(z)): 0.0307 / 0.5605
[1/5][800/1583] Loss_D: 0.6566 Loss_G: 1.7996 D(x): 0.6073 D(G(z)): 0.0531 / 0.2245
[1/5][850/1583] Loss_D: 0.4141 Loss_G: 2.7758 D(x): 0.8372 D(G(z)): 0.1650 / 0.0919
[1/5][900/1583] Loss_D: 0.7488 Loss_G: 4.1499 D(x): 0.8385 D(G(z)): 0.3698 / 0.0261
[1/5][950/1583] Loss_D: 1.0031 Loss_G: 1.6256 D(x): 0.4876 D(G(z)): 0.0742 / 0.2805
[1/5][1000/1583] Loss_D: 0.3197 Loss_G: 3.5365 D(x): 0.9197 D(G(z)): 0.1881 / 0.0426
[1/5][1050/1583] Loss_D: 0.4852 Loss_G: 2.6088 D(x): 0.7459 D(G(z)): 0.1400 / 0.0992
[1/5][1100/1583] Loss_D: 1.4441 Loss_G: 4.7499 D(x): 0.9102 D(G(z)): 0.6548 / 0.0160
[1/5][1150/1583] Loss_D: 0.8372 Loss_G: 3.3722 D(x): 0.8911 D(G(z)): 0.4280 / 0.0614
[1/5][1200/1583] Loss_D: 0.3625 Loss_G: 3.4286 D(x): 0.7971 D(G(z)): 0.0875 / 0.0520
[1/5][1250/1583] Loss_D: 1.7122 Loss_G: 1.5450 D(x): 0.2588 D(G(z)): 0.0382 / 0.3596
[1/5][1300/1583] Loss_D: 0.3812 Loss_G: 2.9381 D(x): 0.9070 D(G(z)): 0.2145 / 0.0863
[1/5][1350/1583] Loss_D: 0.8282 Loss_G: 2.3004 D(x): 0.7097 D(G(z)): 0.2855 / 0.1390
[1/5][1400/1583] Loss_D: 0.6341 Loss_G: 2.8587 D(x): 0.8392 D(G(z)): 0.3181 / 0.0790
[1/5][1450/1583] Loss_D: 0.6178 Loss_G: 1.4617 D(x): 0.6149 D(G(z)): 0.0315 / 0.2863
[1/5][1500/1583] Loss_D: 0.5564 Loss_G: 2.6619 D(x): 0.7793 D(G(z)): 0.2217 / 0.0940
[1/5][1550/1583] Loss_D: 0.6675 Loss_G: 1.9683 D(x): 0.6435 D(G(z)): 0.1213 / 0.1833
[2/5][0/1583] Loss_D: 0.5963 Loss_G: 2.2106 D(x): 0.6437 D(G(z)): 0.0701 / 0.1452
[2/5][50/1583] Loss_D: 1.5170 Loss_G: 4.4082 D(x): 0.9217 D(G(z)): 0.7074 / 0.0197
[2/5][100/1583] Loss_D: 0.4643 Loss_G: 2.4072 D(x): 0.7568 D(G(z)): 0.1341 / 0.1100
[2/5][150/1583] Loss_D: 0.6131 Loss_G: 3.7405 D(x): 0.9036 D(G(z)): 0.3549 / 0.0355
[2/5][200/1583] Loss_D: 0.5679 Loss_G: 2.1571 D(x): 0.6892 D(G(z)): 0.1197 / 0.1484
[2/5][250/1583] Loss_D: 0.6073 Loss_G: 1.5544 D(x): 0.6573 D(G(z)): 0.1079 / 0.2677
[2/5][300/1583] Loss_D: 0.6738 Loss_G: 3.6060 D(x): 0.8955 D(G(z)): 0.3995 / 0.0362
[2/5][350/1583] Loss_D: 0.5477 Loss_G: 2.9593 D(x): 0.8822 D(G(z)): 0.3133 / 0.0710
[2/5][400/1583] Loss_D: 0.4689 Loss_G: 2.2539 D(x): 0.7419 D(G(z)): 0.1151 / 0.1397
[2/5][450/1583] Loss_D: 0.4517 Loss_G: 2.5200 D(x): 0.7845 D(G(z)): 0.1592 / 0.1018
[2/5][500/1583] Loss_D: 0.5757 Loss_G: 2.5563 D(x): 0.7272 D(G(z)): 0.1838 / 0.1009
[2/5][550/1583] Loss_D: 0.5867 Loss_G: 3.2838 D(x): 0.8595 D(G(z)): 0.3113 / 0.0504
[2/5][600/1583] Loss_D: 0.8449 Loss_G: 3.9811 D(x): 0.9381 D(G(z)): 0.4823 / 0.0275
[2/5][650/1583] Loss_D: 0.5224 Loss_G: 1.6869 D(x): 0.7184 D(G(z)): 0.1308 / 0.2290
[2/5][700/1583] Loss_D: 0.7586 Loss_G: 1.4822 D(x): 0.5316 D(G(z)): 0.0298 / 0.2875
[2/5][750/1583] Loss_D: 0.9340 Loss_G: 3.6577 D(x): 0.8168 D(G(z)): 0.4633 / 0.0371
[2/5][800/1583] Loss_D: 0.9857 Loss_G: 4.4083 D(x): 0.9287 D(G(z)): 0.5446 / 0.0168
[2/5][850/1583] Loss_D: 0.5434 Loss_G: 3.0087 D(x): 0.8789 D(G(z)): 0.3096 / 0.0642
[2/5][900/1583] Loss_D: 0.9124 Loss_G: 3.5092 D(x): 0.7808 D(G(z)): 0.4230 / 0.0443
[2/5][950/1583] Loss_D: 0.7267 Loss_G: 4.0834 D(x): 0.8874 D(G(z)): 0.4076 / 0.0246
[2/5][1000/1583] Loss_D: 0.6258 Loss_G: 1.8459 D(x): 0.7038 D(G(z)): 0.1866 / 0.1969
[2/5][1050/1583] Loss_D: 0.9129 Loss_G: 1.5444 D(x): 0.5195 D(G(z)): 0.1200 / 0.2599
[2/5][1100/1583] Loss_D: 0.6557 Loss_G: 3.6323 D(x): 0.9009 D(G(z)): 0.3815 / 0.0375
[2/5][1150/1583] Loss_D: 0.7832 Loss_G: 0.9305 D(x): 0.5585 D(G(z)): 0.0914 / 0.4358
[2/5][1200/1583] Loss_D: 0.4719 Loss_G: 3.0284 D(x): 0.8842 D(G(z)): 0.2650 / 0.0649
[2/5][1250/1583] Loss_D: 0.4804 Loss_G: 2.1393 D(x): 0.7515 D(G(z)): 0.1566 / 0.1427
[2/5][1300/1583] Loss_D: 0.9386 Loss_G: 3.4696 D(x): 0.7883 D(G(z)): 0.4487 / 0.0442
[2/5][1350/1583] Loss_D: 0.4987 Loss_G: 1.7055 D(x): 0.7410 D(G(z)): 0.1531 / 0.2218
[2/5][1400/1583] Loss_D: 0.9054 Loss_G: 4.0416 D(x): 0.9176 D(G(z)): 0.4947 / 0.0277
[2/5][1450/1583] Loss_D: 0.5133 Loss_G: 2.5319 D(x): 0.7986 D(G(z)): 0.2195 / 0.1015
[2/5][1500/1583] Loss_D: 0.7425 Loss_G: 3.2894 D(x): 0.8523 D(G(z)): 0.3979 / 0.0532
[2/5][1550/1583] Loss_D: 0.9294 Loss_G: 1.2275 D(x): 0.4648 D(G(z)): 0.0324 / 0.3599
[3/5][0/1583] Loss_D: 0.9583 Loss_G: 1.1608 D(x): 0.4547 D(G(z)): 0.0335 / 0.3771
[3/5][50/1583] Loss_D: 0.8272 Loss_G: 1.7047 D(x): 0.5949 D(G(z)): 0.1800 / 0.2317
[3/5][100/1583] Loss_D: 0.5761 Loss_G: 3.6231 D(x): 0.8937 D(G(z)): 0.3400 / 0.0367
[3/5][150/1583] Loss_D: 0.6144 Loss_G: 1.0569 D(x): 0.6247 D(G(z)): 0.0867 / 0.3969
[3/5][200/1583] Loss_D: 0.6703 Loss_G: 1.9168 D(x): 0.7176 D(G(z)): 0.2415 / 0.1718
[3/5][250/1583] Loss_D: 0.4968 Loss_G: 2.6420 D(x): 0.7417 D(G(z)): 0.1436 / 0.1051
[3/5][300/1583] Loss_D: 0.7349 Loss_G: 0.8902 D(x): 0.5783 D(G(z)): 0.0955 / 0.4540
[3/5][350/1583] Loss_D: 0.7369 Loss_G: 2.7404 D(x): 0.7916 D(G(z)): 0.3492 / 0.0855
[3/5][400/1583] Loss_D: 0.6515 Loss_G: 2.8947 D(x): 0.7512 D(G(z)): 0.2633 / 0.0773
[3/5][450/1583] Loss_D: 0.6572 Loss_G: 1.6984 D(x): 0.6819 D(G(z)): 0.1973 / 0.2194
[3/5][500/1583] Loss_D: 0.6705 Loss_G: 1.9898 D(x): 0.6495 D(G(z)): 0.1540 / 0.1725
[3/5][550/1583] Loss_D: 0.5451 Loss_G: 2.4617 D(x): 0.8146 D(G(z)): 0.2534 / 0.1119
[3/5][600/1583] Loss_D: 0.5778 Loss_G: 2.8757 D(x): 0.7501 D(G(z)): 0.2017 / 0.0799
[3/5][650/1583] Loss_D: 0.5724 Loss_G: 2.1972 D(x): 0.7264 D(G(z)): 0.1839 / 0.1486
[3/5][700/1583] Loss_D: 1.2302 Loss_G: 4.5527 D(x): 0.9450 D(G(z)): 0.6299 / 0.0161
[3/5][750/1583] Loss_D: 0.6716 Loss_G: 2.0258 D(x): 0.6407 D(G(z)): 0.1369 / 0.1712
[3/5][800/1583] Loss_D: 0.5515 Loss_G: 2.1855 D(x): 0.7735 D(G(z)): 0.2209 / 0.1395
[3/5][850/1583] Loss_D: 1.6550 Loss_G: 5.3041 D(x): 0.9557 D(G(z)): 0.7417 / 0.0082
[3/5][900/1583] Loss_D: 1.5012 Loss_G: 6.1913 D(x): 0.9689 D(G(z)): 0.6948 / 0.0041
[3/5][950/1583] Loss_D: 0.4969 Loss_G: 2.7285 D(x): 0.8293 D(G(z)): 0.2401 / 0.0846
[3/5][1000/1583] Loss_D: 0.6695 Loss_G: 1.8164 D(x): 0.6038 D(G(z)): 0.0651 / 0.2048
[3/5][1050/1583] Loss_D: 0.5644 Loss_G: 1.7400 D(x): 0.7405 D(G(z)): 0.1959 / 0.2097
[3/5][1100/1583] Loss_D: 0.8853 Loss_G: 1.6351 D(x): 0.5643 D(G(z)): 0.1673 / 0.2550
[3/5][1150/1583] Loss_D: 1.6414 Loss_G: 0.4946 D(x): 0.2512 D(G(z)): 0.0278 / 0.6601
[3/5][1200/1583] Loss_D: 0.9217 Loss_G: 0.7732 D(x): 0.4728 D(G(z)): 0.0525 / 0.5116
[3/5][1250/1583] Loss_D: 0.8338 Loss_G: 1.5767 D(x): 0.5083 D(G(z)): 0.0630 / 0.2551
[3/5][1300/1583] Loss_D: 0.7982 Loss_G: 3.7209 D(x): 0.8877 D(G(z)): 0.4442 / 0.0361
[3/5][1350/1583] Loss_D: 0.4342 Loss_G: 2.7570 D(x): 0.8195 D(G(z)): 0.1871 / 0.0820
[3/5][1400/1583] Loss_D: 0.5983 Loss_G: 3.2100 D(x): 0.8487 D(G(z)): 0.3273 / 0.0523
[3/5][1450/1583] Loss_D: 0.6556 Loss_G: 2.2088 D(x): 0.6753 D(G(z)): 0.1843 / 0.1396
[3/5][1500/1583] Loss_D: 1.4272 Loss_G: 4.3660 D(x): 0.9378 D(G(z)): 0.6743 / 0.0210
[3/5][1550/1583] Loss_D: 0.6038 Loss_G: 2.4530 D(x): 0.7970 D(G(z)): 0.2745 / 0.1143
[4/5][0/1583] Loss_D: 1.0254 Loss_G: 3.7756 D(x): 0.8369 D(G(z)): 0.5216 / 0.0385
[4/5][50/1583] Loss_D: 0.6841 Loss_G: 2.9326 D(x): 0.8038 D(G(z)): 0.3241 / 0.0689
[4/5][100/1583] Loss_D: 0.6353 Loss_G: 1.5868 D(x): 0.6100 D(G(z)): 0.0740 / 0.2480
[4/5][150/1583] Loss_D: 2.2435 Loss_G: 3.7620 D(x): 0.9507 D(G(z)): 0.8368 / 0.0387
[4/5][200/1583] Loss_D: 0.6184 Loss_G: 1.8196 D(x): 0.6856 D(G(z)): 0.1562 / 0.1994
[4/5][250/1583] Loss_D: 0.5574 Loss_G: 1.8185 D(x): 0.6915 D(G(z)): 0.1294 / 0.1960
[4/5][300/1583] Loss_D: 0.5771 Loss_G: 3.4464 D(x): 0.9116 D(G(z)): 0.3473 / 0.0430
[4/5][350/1583] Loss_D: 0.5368 Loss_G: 3.0320 D(x): 0.8551 D(G(z)): 0.2862 / 0.0643
[4/5][400/1583] Loss_D: 0.7641 Loss_G: 1.4842 D(x): 0.5538 D(G(z)): 0.0720 / 0.2773
[4/5][450/1583] Loss_D: 0.8868 Loss_G: 4.3501 D(x): 0.9490 D(G(z)): 0.5257 / 0.0173
[4/5][500/1583] Loss_D: 1.0951 Loss_G: 1.1540 D(x): 0.4149 D(G(z)): 0.0316 / 0.3755
[4/5][550/1583] Loss_D: 0.5921 Loss_G: 3.2704 D(x): 0.8644 D(G(z)): 0.3268 / 0.0504
[4/5][600/1583] Loss_D: 1.9290 Loss_G: 0.0810 D(x): 0.2260 D(G(z)): 0.0389 / 0.9277
[4/5][650/1583] Loss_D: 0.5085 Loss_G: 2.6994 D(x): 0.8242 D(G(z)): 0.2472 / 0.0845
[4/5][700/1583] Loss_D: 0.7072 Loss_G: 1.5190 D(x): 0.5953 D(G(z)): 0.0826 / 0.2650
[4/5][750/1583] Loss_D: 0.5817 Loss_G: 2.7395 D(x): 0.8310 D(G(z)): 0.2830 / 0.0853
[4/5][800/1583] Loss_D: 0.4707 Loss_G: 2.3596 D(x): 0.7818 D(G(z)): 0.1635 / 0.1262
[4/5][850/1583] Loss_D: 1.6073 Loss_G: 0.4274 D(x): 0.2876 D(G(z)): 0.0989 / 0.6886
[4/5][900/1583] Loss_D: 0.5918 Loss_G: 2.6160 D(x): 0.7312 D(G(z)): 0.1983 / 0.0984
[4/5][950/1583] Loss_D: 0.7132 Loss_G: 2.7998 D(x): 0.8739 D(G(z)): 0.3872 / 0.0858
[4/5][1000/1583] Loss_D: 0.8327 Loss_G: 3.9972 D(x): 0.9455 D(G(z)): 0.4914 / 0.0265
[4/5][1050/1583] Loss_D: 0.4837 Loss_G: 2.4716 D(x): 0.7829 D(G(z)): 0.1792 / 0.1073
[4/5][1100/1583] Loss_D: 0.7168 Loss_G: 1.8686 D(x): 0.6250 D(G(z)): 0.1307 / 0.1945
[4/5][1150/1583] Loss_D: 0.5136 Loss_G: 2.0851 D(x): 0.7486 D(G(z)): 0.1614 / 0.1606
[4/5][1200/1583] Loss_D: 0.4791 Loss_G: 2.0791 D(x): 0.7381 D(G(z)): 0.1236 / 0.1586
[4/5][1250/1583] Loss_D: 0.5550 Loss_G: 2.5631 D(x): 0.8379 D(G(z)): 0.2759 / 0.1006
[4/5][1300/1583] Loss_D: 0.3853 Loss_G: 3.4606 D(x): 0.9458 D(G(z)): 0.2601 / 0.0419
[4/5][1350/1583] Loss_D: 0.6888 Loss_G: 3.2058 D(x): 0.8515 D(G(z)): 0.3644 / 0.0533
[4/5][1400/1583] Loss_D: 0.8042 Loss_G: 4.1665 D(x): 0.9471 D(G(z)): 0.4778 / 0.0235
[4/5][1450/1583] Loss_D: 0.4398 Loss_G: 1.8515 D(x): 0.7708 D(G(z)): 0.1293 / 0.1916
[4/5][1500/1583] Loss_D: 2.1083 Loss_G: 0.3365 D(x): 0.1914 D(G(z)): 0.0699 / 0.7397
[4/5][1550/1583] Loss_D: 0.6472 Loss_G: 1.5645 D(x): 0.6363 D(G(z)): 0.1143 / 0.2488
结果¶
最后,让我们看看我们的训练结果如何。在这里,我们将查看三种不同的结果。首先,我们将看到 D 和 G 的损失在训练过程中如何变化。其次,我们将可视化每个 epoch 中 G 在 fixed_noise 批次上的输出。第三,我们将并排查看一批真实数据和一批 G 生成的假数据。
损失与训练迭代次数的关系
下方是 D & G 的损失与训练迭代次数的关系图。
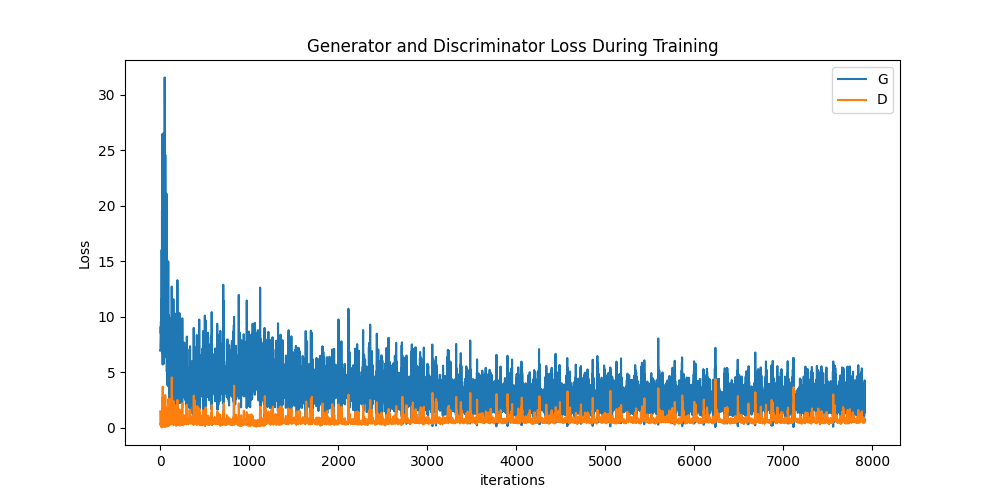
G 进展的可视化
还记得我们在每个训练 epoch 结束后都保存了生成器在 fixed_noise 批次上的输出吗?现在,我们可以通过动画来可视化 G 的训练进展。按下播放按钮开始动画。
fig = plt.figure(figsize=(8,8))
plt.axis("off")
ims = [[plt.imshow(np.transpose(i,(1,2,0)), animated=True)] for i in img_list]
ani = animation.ArtistAnimation(fig, ims, interval=1000, repeat_delay=1000, blit=True)
HTML(ani.to_jshtml())



