强化学习 (DQN) 教程

创建于: 2017 年 3 月 24 日 | 最后更新于: 2024 年 6 月 18 日 | 最后验证于: 2024 年 11 月 5 日

作者: Adam Paszke

Mark Towers

本教程展示了如何使用 PyTorch 在 Gymnasium 中的 CartPole-v1 任务上训练一个深度 Q 学习 (DQN) 智能体。

你可能会发现阅读原始的 深度 Q 学习 (DQN) 论文有所帮助

任务

智能体必须在两个动作之间做出决定——向左或向右移动推车——以便连接在上面的杆子保持直立。你可以在 Gymnasium 的网站上找到有关该环境以及其他更具挑战性环境的更多信息。

CartPole（倒立摆）

当智能体观察环境的当前状态并选择一个动作时，环境会迁移到新的状态，并返回一个奖励，该奖励表明了动作的后果。在该任务中，每增加一个时间步，奖励为 +1；如果杆子倾倒得太远或推车偏离中心超过 2.4 个单位，环境就会终止。这意味着表现更好的场景将运行更长时间，累积更大的回报。

CartPole 任务的设计使得智能体的输入是代表环境状态（位置、速度等）的 4 个实数值。我们将这 4 个输入不做任何缩放，直接通过一个具有 2 个输出的小型全连接网络，每个输出对应一个动作。网络经过训练，可以根据输入状态预测每个动作的期望值。然后选择具有最高期望值的动作。

软件包

首先，让我们导入所需的软件包。首先，我们需要用于环境的 gymnasium，使用 pip 安装。这是原始 OpenAI Gym 项目的一个分支，自 Gym v0.19 以来由同一个团队维护。如果你在 Google Colab 中运行此代码，请运行

%%bash
pip3 install gymnasium[classic_control]

我们还将使用 PyTorch 中的以下内容：

• 神经网络 (torch.nn)

• 优化 (torch.optim)

• 自动微分 (torch.autograd)

import gymnasium as gym
import math
import random
import matplotlib
import matplotlib.pyplot as plt
from collections import namedtuple, deque
from itertools import count

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F

env = gym.make("CartPole-v1")

# set up matplotlib
is_ipython = 'inline' in matplotlib.get_backend()
if is_ipython:
    from IPython import display

plt.ion()

# if GPU is to be used
device = torch.device(
    "cuda" if torch.cuda.is_available() else
    "mps" if torch.backends.mps.is_available() else
    "cpu"
)

回放缓冲区

我们将使用经验回放缓冲区来训练 DQN。它存储智能体观察到的转移（transitions），使我们以后可以重用这些数据。通过从中随机采样，构建批次的转移之间会去相关。这已被证明可以极大地稳定和改进 DQN 训练过程。

为此，我们需要两个类：

• Transition - 一个命名元组，表示环境中的单个转移。它本质上将 (state, action) 对映射到它们的 (next_state, reward) 结果，其中状态是稍后描述的屏幕差分图像。

• ReplayMemory - 一个有限大小的循环缓冲区，用于存储最近观察到的转移。它还实现了一个 .sample() 方法，用于随机选择一批转移进行训练。

Transition = namedtuple('Transition',
                        ('state', 'action', 'next_state', 'reward'))


class ReplayMemory(object):

    def __init__(self, capacity):
        self.memory = deque([], maxlen=capacity)

    def push(self, *args):
        """Save a transition"""
        self.memory.append(Transition(*args))

    def sample(self, batch_size):
        return random.sample(self.memory, batch_size)

    def __len__(self):
        return len(self.memory)

现在，让我们定义模型。但首先，快速回顾一下 DQN 是什么。

DQN 算法

我们的环境是确定性的，因此为了简单起见，这里展示的所有方程也都是确定性地构建的。在强化学习文献中，它们通常还包含对环境中随机转移的期望。

我们的目标是训练一个策略，使其尝试最大化折扣累积奖励 \(R_{t_0} = \sum_{t=t_0}^{\infty} \gamma^{t - t_0} r_t\)，其中 \(R_{t_0}\) 也称为回报 (return)。折扣因子 \(\gamma\) 应该是一个介于 \(0\) 和 \(1\) 之间的常数，确保求和收敛。较低的 \(\gamma\) 使得不确定遥远未来的奖励相对于可以相当确定的近期奖励对智能体而言不那么重要。它也鼓励智能体获取时间上更近的奖励，而不是时间上遥远未来等价的奖励。

Q 学习背后的主要思想是，如果我们有一个函数 \(Q^*: 状态 \times 动作 \rightarrow \mathbb{R}\)，它可以告诉我们在给定状态下采取某个动作后，我们的回报将是多少，那么我们就可以轻松构建一个最大化奖励的策略：

\[\pi^*(s) = \arg\!\max_a \ Q^*(s, a) \ ]

然而，我们并不了解世界的一切，因此无法直接获取 \(Q^*\)。但是，由于神经网络是万能函数逼近器，我们可以简单地创建一个神经网络并训练它来模拟 \(Q^*\)。

对于我们的训练更新规则，我们将利用这样一个事实：任何策略的 \(Q\) 函数都遵循 Bellman 方程：

\[Q^{\pi}(s, a) = r + \gamma Q^{\pi}(s', \pi(s')) \ ]

等式两边的差值称为时序差分误差 \(\delta\)：

\[\delta = Q(s, a) - (r + \gamma \max_a' Q(s', a)) \ ]

为了最小化这个误差，我们将使用 Huber 损失。Huber 损失在误差较小时表现得像均方误差，在误差较大时则像平均绝对误差——这使得它在 \(Q\) 的估计值非常嘈杂时对异常值更具鲁棒性。我们在从回放缓冲区中采样的一批转移 \(B\) 上计算这个损失：

\[\mathcal{L} = \frac{1}{|B|}\sum_{(s, a, s', r) \ \in \ B} \mathcal{L}(\delta)\]

\[\text{where} \quad \mathcal{L}(\delta) = \begin{cases} \frac{1}{2}{\delta^2} & \text{for } |\delta| \le 1, \\ |\delta| - \frac{1}{2} & \text{otherwise.} \end{cases}\]

Q 网络

我们的模型将是一个前馈神经网络，它接收当前屏幕补丁与先前屏幕补丁之间的差异作为输入。它有两个输出，分别代表 \(Q(s, \mathrm{left})\) 和 \(Q(s, \mathrm{right})\)（其中 \(s\) 是网络的输入）。实际上，网络试图预测在当前输入下采取每个动作的期望回报。

class DQN(nn.Module):

    def __init__(self, n_observations, n_actions):
        super(DQN, self).__init__()
        self.layer1 = nn.Linear(n_observations, 128)
        self.layer2 = nn.Linear(128, 128)
        self.layer3 = nn.Linear(128, n_actions)

    # Called with either one element to determine next action, or a batch
    # during optimization. Returns tensor([[left0exp,right0exp]...]).
    def forward(self, x):
        x = F.relu(self.layer1(x))
        x = F.relu(self.layer2(x))
        return self.layer3(x)

训练

超参数和辅助函数

此单元实例化了我们的模型及其优化器，并定义了一些辅助函数：

• select_action - 将根据 ε-greedy 策略选择一个动作。简单来说，我们有时会使用模型来选择动作，有时会均匀采样一个动作。选择随机动作的概率将从 EPS_START 开始，并指数衰减到 EPS_END。EPS_DECAY 控制衰减速率。

• plot_durations - 一个辅助函数，用于绘制每回合的持续时间，以及过去 100 回合的平均值（这是官方评估中使用的衡量标准）。图表将位于包含主训练循环的单元格下方，并在每回合后更新。

# BATCH_SIZE is the number of transitions sampled from the replay buffer
# GAMMA is the discount factor as mentioned in the previous section
# EPS_START is the starting value of epsilon
# EPS_END is the final value of epsilon
# EPS_DECAY controls the rate of exponential decay of epsilon, higher means a slower decay
# TAU is the update rate of the target network
# LR is the learning rate of the ``AdamW`` optimizer
BATCH_SIZE = 128
GAMMA = 0.99
EPS_START = 0.9
EPS_END = 0.05
EPS_DECAY = 1000
TAU = 0.005
LR = 1e-4

# Get number of actions from gym action space
n_actions = env.action_space.n
# Get the number of state observations
state, info = env.reset()
n_observations = len(state)

policy_net = DQN(n_observations, n_actions).to(device)
target_net = DQN(n_observations, n_actions).to(device)
target_net.load_state_dict(policy_net.state_dict())

optimizer = optim.AdamW(policy_net.parameters(), lr=LR, amsgrad=True)
memory = ReplayMemory(10000)


steps_done = 0


def select_action(state):
    global steps_done
    sample = random.random()
    eps_threshold = EPS_END + (EPS_START - EPS_END) * \
        math.exp(-1. * steps_done / EPS_DECAY)
    steps_done += 1
    if sample > eps_threshold:
        with torch.no_grad():
            # t.max(1) will return the largest column value of each row.
            # second column on max result is index of where max element was
            # found, so we pick action with the larger expected reward.
            return policy_net(state).max(1).indices.view(1, 1)
    else:
        return torch.tensor([[env.action_space.sample()]], device=device, dtype=torch.long)


episode_durations = []


def plot_durations(show_result=False):
    plt.figure(1)
    durations_t = torch.tensor(episode_durations, dtype=torch.float)
    if show_result:
        plt.title('Result')
    else:
        plt.clf()
        plt.title('Training...')
    plt.xlabel('Episode')
    plt.ylabel('Duration')
    plt.plot(durations_t.numpy())
    # Take 100 episode averages and plot them too
    if len(durations_t) >= 100:
        means = durations_t.unfold(0, 100, 1).mean(1).view(-1)
        means = torch.cat((torch.zeros(99), means))
        plt.plot(means.numpy())

    plt.pause(0.001)  # pause a bit so that plots are updated
    if is_ipython:
        if not show_result:
            display.display(plt.gcf())
            display.clear_output(wait=True)
        else:
            display.display(plt.gcf())

训练循环

最后是训练模型的代码。

在这里，你可以找到执行单步优化的 optimize_model 函数。它首先采样一批数据，将所有张量连接成一个，计算 \(Q(s_t, a_t)\) 和 \(V(s_{t+1}) = \max_a Q(s_{t+1}, a)\)，并将它们组合成我们的损失。根据定义，如果 \(s\) 是终止状态，我们将 \(V(s)\) 设置为 0。我们还使用一个目标网络来计算 \(V(s_{t+1})\) 以增加稳定性。目标网络在每一步都会通过超参数 TAU 控制的软更新进行更新，该超参数之前已定义。

def optimize_model():
    if len(memory) < BATCH_SIZE:
        return
    transitions = memory.sample(BATCH_SIZE)
    # Transpose the batch (see https://stackoverflow.com/a/19343/3343043 for
    # detailed explanation). This converts batch-array of Transitions
    # to Transition of batch-arrays.
    batch = Transition(*zip(*transitions))

    # Compute a mask of non-final states and concatenate the batch elements
    # (a final state would've been the one after which simulation ended)
    non_final_mask = torch.tensor(tuple(map(lambda s: s is not None,
                                          batch.next_state)), device=device, dtype=torch.bool)
    non_final_next_states = torch.cat([s for s in batch.next_state
                                                if s is not None])
    state_batch = torch.cat(batch.state)
    action_batch = torch.cat(batch.action)
    reward_batch = torch.cat(batch.reward)

    # Compute Q(s_t, a) - the model computes Q(s_t), then we select the
    # columns of actions taken. These are the actions which would've been taken
    # for each batch state according to policy_net
    state_action_values = policy_net(state_batch).gather(1, action_batch)

    # Compute V(s_{t+1}) for all next states.
    # Expected values of actions for non_final_next_states are computed based
    # on the "older" target_net; selecting their best reward with max(1).values
    # This is merged based on the mask, such that we'll have either the expected
    # state value or 0 in case the state was final.
    next_state_values = torch.zeros(BATCH_SIZE, device=device)
    with torch.no_grad():
        next_state_values[non_final_mask] = target_net(non_final_next_states).max(1).values
    # Compute the expected Q values
    expected_state_action_values = (next_state_values * GAMMA) + reward_batch

    # Compute Huber loss
    criterion = nn.SmoothL1Loss()
    loss = criterion(state_action_values, expected_state_action_values.unsqueeze(1))

    # Optimize the model
    optimizer.zero_grad()
    loss.backward()
    # In-place gradient clipping
    torch.nn.utils.clip_grad_value_(policy_net.parameters(), 100)
    optimizer.step()

下面是主训练循环。开始时，我们重置环境并获取初始 state 张量。然后，我们采样一个动作，执行它，观察下一个状态和奖励（总是 1），并优化模型一次。当回合结束（模型失败）时，我们重新开始循环。

在下面，如果 GPU 可用，num_episodes 设置为 600，否则安排 50 回合，以便训练不会花费太长时间。然而，50 回合不足以观察到 CartPole 上的良好性能。你应该会看到模型在 600 个训练回合内持续达到 500 步。训练强化学习智能体可能是一个嘈杂的过程，因此如果未观察到收敛，重新开始训练可能会产生更好的结果。

if torch.cuda.is_available() or torch.backends.mps.is_available():
    num_episodes = 600
else:
    num_episodes = 50

for i_episode in range(num_episodes):
    # Initialize the environment and get its state
    state, info = env.reset()
    state = torch.tensor(state, dtype=torch.float32, device=device).unsqueeze(0)
    for t in count():
        action = select_action(state)
        observation, reward, terminated, truncated, _ = env.step(action.item())
        reward = torch.tensor([reward], device=device)
        done = terminated or truncated

        if terminated:
            next_state = None
        else:
            next_state = torch.tensor(observation, dtype=torch.float32, device=device).unsqueeze(0)

        # Store the transition in memory
        memory.push(state, action, next_state, reward)

        # Move to the next state
        state = next_state

        # Perform one step of the optimization (on the policy network)
        optimize_model()

        # Soft update of the target network's weights
        # θ′ ← τ θ + (1 −τ )θ′
        target_net_state_dict = target_net.state_dict()
        policy_net_state_dict = policy_net.state_dict()
        for key in policy_net_state_dict:
            target_net_state_dict[key] = policy_net_state_dict[key]*TAU + target_net_state_dict[key]*(1-TAU)
        target_net.load_state_dict(target_net_state_dict)

        if done:
            episode_durations.append(t + 1)
            plot_durations()
            break

print('Complete')
plot_durations(show_result=True)
plt.ioff()
plt.show()

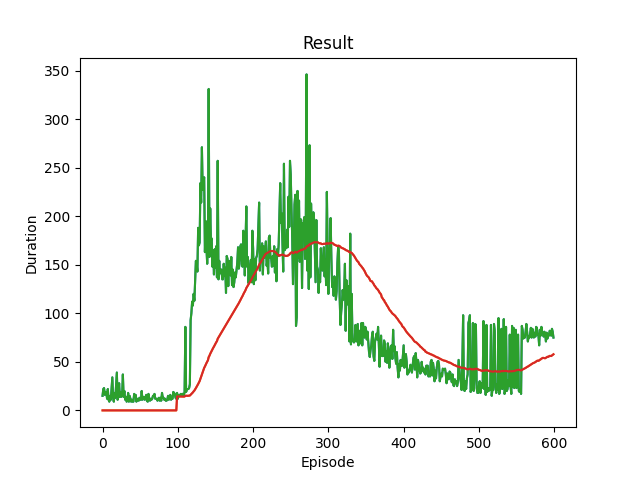
/usr/local/lib/python3.10/dist-packages/gymnasium/utils/passive_env_checker.py:249: DeprecationWarning:

`np.bool8` is a deprecated alias for `np.bool_`.  (Deprecated NumPy 1.24)

Complete

这里是说明整体数据流的图示。

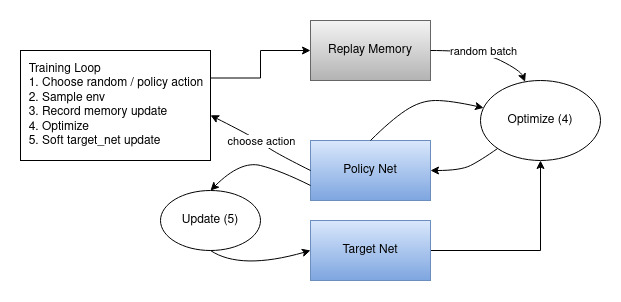
动作随机选择或基于策略选择，从 gym 环境获取下一步样本。我们将结果记录在回放缓冲区中，并在每次迭代时运行优化步骤。优化从回放缓冲区中随机选取一批数据来训练新策略。“较旧的” target_net 也用于优化中计算期望的 Q 值。每一步都会对其权重进行软更新。