autograd 保存的张量的钩子

创建于： Nov 03, 2021 | 最后更新于： Aug 27, 2024 | 最后验证于： 未验证

PyTorch 通常使用反向传播计算梯度。然而，某些操作需要保存中间结果以便执行反向传播。本教程将详细介绍如何保存/检索这些张量，以及如何定义钩子来控制打包/解包过程。

本教程假设您熟悉反向传播的理论工作原理。如果还不熟悉，请先阅读这篇文章。

保存的张量

训练模型通常比运行推理消耗更多内存。从广义上讲，可以说这是因为“PyTorch 需要保存计算图，这对于调用 backward 是必需的”，因此增加了内存使用量。本教程的一个目标是微调这种理解。

事实上，图本身有时不会消耗更多内存，因为它从不复制任何张量。然而，图可以保留对张量的引用，否则这些张量就会超出作用域：这些引用被称为保存的张量。

为什么训练模型通常比评估模型需要更多内存？

我们从一个简单的例子开始：\(y = a \cdot b\)，我们知道 \(y\) 关于 \(a\) 和 \(b\) 的梯度：

\[\frac{\partial y}{\partial a} = b \]

\[\frac{\partial y}{\partial b} = a \]

import torch

a = torch.randn(5, requires_grad=True)
b = torch.ones(5, requires_grad=True)
y = a * b

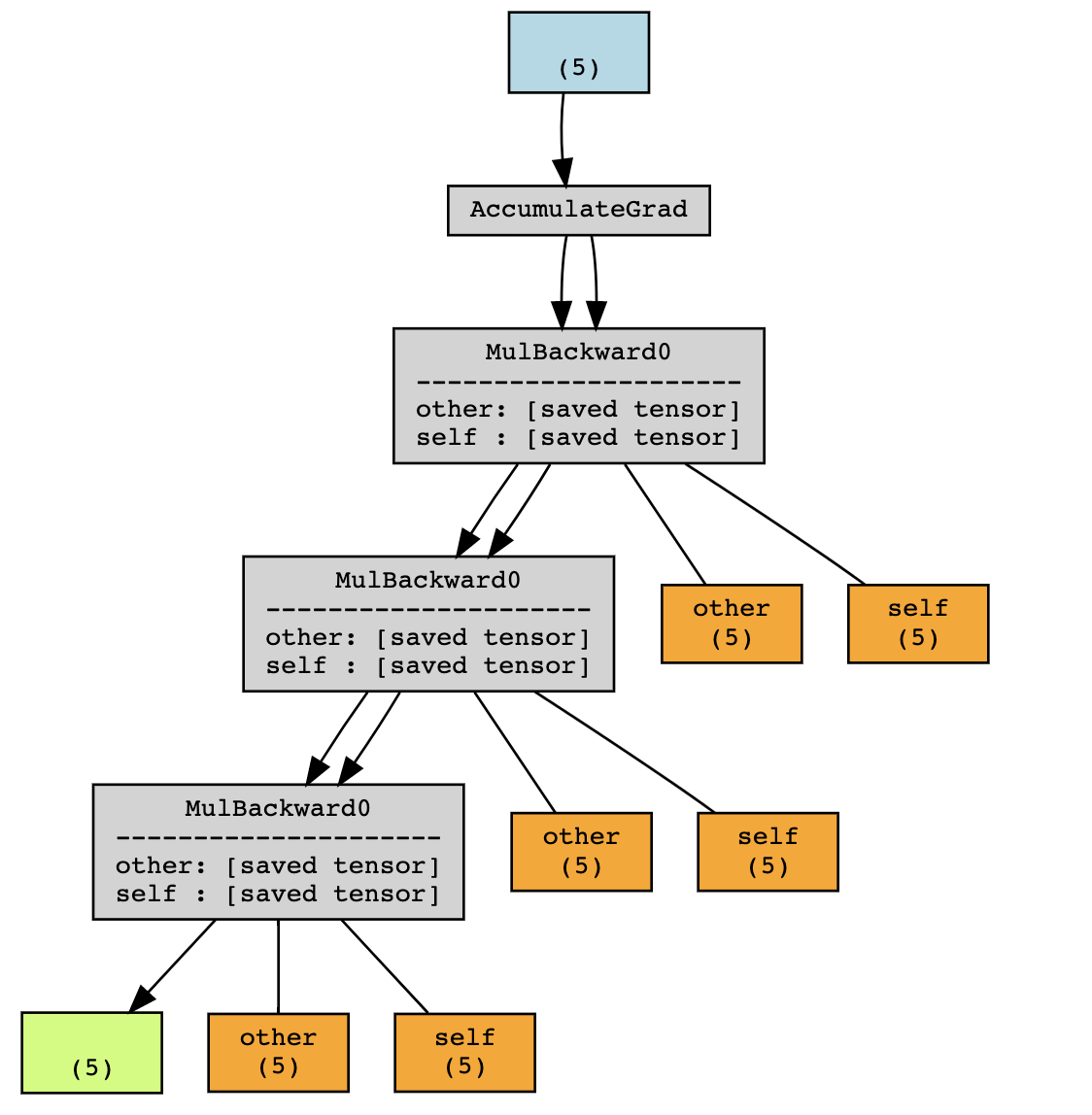
使用 torchviz，我们可以可视化计算图

在此示例中，PyTorch 保存中间值 \(a\) 和 \(b\)，以便在反向传播期间计算梯度。

这些中间值（在上图中呈橙色）可以通过查找 y 的 grad_fn 中以 _saved 为前缀的属性来访问（出于调试目的）

print(y.grad_fn._saved_self)
print(y.grad_fn._saved_other)

tensor([ 0.3367,  0.1288,  0.2345,  0.2303, -1.1229], requires_grad=True)
tensor([1., 1., 1., 1., 1.], requires_grad=True)

随着计算图的深度增加，它将存储更多保存的张量。同时，如果不是因为图，这些张量就会超出作用域。

def f(x):
    return x * x

x = torch.randn(5, requires_grad=True)
y = f(f(f(x)))

在上面的例子中，在没有 grad 的情况下执行只会将 x 和 y 保留在作用域内，但图还会额外存储 f(x) 和 f(f(x))。因此，训练期间运行前向传播将比评估期间消耗更多内存（更准确地说，是在不需要 autograd 的时候）。

打包/解包的概念

回到第一个例子：y.grad_fn._saved_self 和 y.grad_fn._saved_other 分别指向原始张量对象 a 和 b。

a = torch.randn(5, requires_grad=True)
b = torch.ones(5, requires_grad=True)
y = a * b

print(y.grad_fn._saved_self is a)   # True
print(y.grad_fn._saved_other is b)  # True

True
True

然而，情况并非总是如此。

a = torch.randn(5, requires_grad=True)
y = torch.exp(a)
print(y.grad_fn._saved_result.equal(y))  # True
print(y.grad_fn._saved_result is y)      # False

True
False

在底层，PyTorch 对张量 y 进行了打包和解包操作，以防止引用循环。

通常来说，您不应该依赖于访问为反向传播保存的张量会得到与原始张量相同的张量对象。然而，它们将共享相同的存储。

保存的张量钩子

PyTorch 提供了一个 API 来控制如何打包/解包保存的张量。

def pack_hook(x):
    print("Packing", x)
    return x

def unpack_hook(x):
    print("Unpacking", x)
    return x
a = torch.ones(5, requires_grad=True)
b = torch.ones(5, requires_grad=True) * 2

with torch.autograd.graph.saved_tensors_hooks(pack_hook, unpack_hook):
    y = a * b

y.sum().backward()

Packing tensor([2., 2., 2., 2., 2.], grad_fn=<MulBackward0>)
Packing tensor([1., 1., 1., 1., 1.], requires_grad=True)
Unpacking tensor([2., 2., 2., 2., 2.], grad_fn=<MulBackward0>)
Unpacking tensor([1., 1., 1., 1., 1.], requires_grad=True)

pack_hook 函数将在每次操作为反向传播保存张量时调用。pack_hook 的输出随后存储在计算图中，而不是原始张量。unpack_hook 使用该返回值计算一个新的张量，该张量是在反向传播过程中实际使用的张量。通常，您希望 unpack_hook(pack_hook(t)) 等于 t。

x = torch.randn(5, requires_grad=True)
with torch.autograd.graph.saved_tensors_hooks(lambda x: x * 4, lambda x: x / 4):
    y = torch.pow(x, 2)
y.sum().backward()
assert(x.grad.equal(2 * x))

需要注意的是，pack_hook 的输出可以是任何 Python 对象，只要 unpack_hook 可以从中派生出具有正确值的张量即可。

一些非常规示例

首先，一些愚蠢的例子来说明什么是可能的，但你可能永远不想这样做。

返回一个 int

返回 Python 列表的索引 相对无害，但实用性值得商榷

storage = []

def pack(x):
    storage.append(x)
    return len(storage) - 1

def unpack(x):
    return storage[x]

x = torch.randn(5, requires_grad=True)
with torch.autograd.graph.saved_tensors_hooks(pack, unpack):
    y = x * x
y.sum().backward()

assert(x.grad.equal(2 * x))

返回一个元组

返回某个张量以及如何解包它的函数 以当前形式来看，不太可能有用

def pack(x):
    delta = torch.randn(*x.size())
    return x - delta, lambda x: x + delta

def unpack(packed):
    x, f = packed
    return f(x)


x = torch.randn(5, requires_grad=True)
with torch.autograd.graph.saved_tensors_hooks(pack, unpack):
    y = x * x
y.sum().backward()

assert(torch.allclose(x.grad, 2 * x))

返回一个 str

返回张量的 __repr__ 可能永远不要这样做

x = torch.randn(5, requires_grad=True)
with torch.autograd.graph.saved_tensors_hooks(lambda x: repr(x), lambda x: eval("torch." + x)):
    y = x * x
y.sum().backward()
assert(torch.all(x.grad - 2 * x <= 1e-4))

尽管这些例子在实践中没有用，但它们说明 pack_hook 的输出确实可以是任何 Python 对象，只要它包含足够的信息来检索原始张量的内容。在下一节中，我们将重点介绍更有用的应用。

将张量保存到 CPU

很多时候，计算图中涉及的张量位于 GPU 上。在图中保留对这些张量的引用是导致大多数模型在训练期间 GPU 内存不足的原因，而它们在评估期间会运行良好。

钩子提供了一种非常简单的方式来实现这一点。

def pack_hook(x):
    return (x.device, x.cpu())

def unpack_hook(packed):
    device, tensor = packed
    return tensor.to(device)

x = torch.randn(5, requires_grad=True)
with torch.autograd.graph.saved_tensors_hooks(pack, unpack):
    y = x * x
y.sum().backward()

torch.allclose(x.grad, (2 * x))

True

事实上，PyTorch 提供了一个 API 来方便地使用这些钩子（以及使用固定内存的功能）。

import torch.nn as nn

class Model(nn.Module):
    def __init__(self):
        super().__init__()
        self.w = nn.Parameter(torch.randn(5))

    def forward(self, x):
        with torch.autograd.graph.save_on_cpu(pin_memory=True):
            # some computation
            return self.w * x

x = torch.randn(5)
model = Model()
loss = model(x).sum()
loss.backward()

在实践中，在 A100 GPU 上，对于 ResNet-152，批量大小为 256 时，这对应于 GPU 内存使用量从 48GB 减少到 5GB，代价是速度减慢 6 倍。

当然，您可以通过只将网络的某些部分保存到 CPU 来调整这种权衡。

例如，您可以定义一个特殊的 nn.Module，它包装任何模块并将其张量保存到 CPU。

class SaveToCpu(nn.Module):
    def __init__(self, module):
        super().__init__()
        self.module = module

    def forward(self, *args, **kwargs):
        with torch.autograd.graph.save_on_cpu(pin_memory=True):
            return self.module(*args, **kwargs)

model = nn.Sequential(
    nn.Linear(10, 100),
    SaveToCpu(nn.Linear(100, 100)),
    nn.Linear(100, 10),
)

x = torch.randn(10)
loss = model(x).sum()
loss.backward()

将张量保存到磁盘

类似地，您可能希望将这些张量保存到磁盘。同样，这可以使用这些钩子实现。

一个简单的版本如下所示。

# Naive version - HINT: Don't do this

import uuid
tmp_dir = "temp"

def pack_hook(tensor):
    name = os.path.join(tmp_dir, str(uuid.uuid4()))
    torch.save(tensor, name)
    return name

def unpack_hook(name):
    return torch.load(name, weights_only=True)

上面代码的问题在于我们在磁盘上泄露了文件，并且它们从未被清除。修复这个问题并不像看起来那么简单。

# Incorrect version - HINT: Don't do this

import uuid
import os
import tempfile
tmp_dir_obj = tempfile.TemporaryDirectory()
tmp_dir = tmp_dir_obj.name

def pack_hook(tensor):
    name = os.path.join(tmp_dir, str(uuid.uuid4()))
    torch.save(tensor, name)
    return name

def unpack_hook(name):
    tensor = torch.load(name, weights_only=True)
    os.remove(name)
    return tensor

上面代码不起作用的原因是 unpack_hook 可以被多次调用。如果我们第一次解包时删除了文件，当第二次访问保存的张量时，它将不可用，这将引发错误。

x = torch.ones(5, requires_grad=True)
with torch.autograd.graph.saved_tensors_hooks(pack_hook, unpack_hook):
    y = x.pow(2)
print(y.grad_fn._saved_self)
try:
    print(y.grad_fn._saved_self)
    print("Double access succeeded!")
except:
    print("Double access failed!")

tensor([1., 1., 1., 1., 1.], requires_grad=True)
Double access failed!

为了解决这个问题，我们可以编写一个版本的钩子，利用 PyTorch 在不再需要时会自动释放（删除）保存的数据这一事实。

class SelfDeletingTempFile():
    def __init__(self):
        self.name = os.path.join(tmp_dir, str(uuid.uuid4()))

    def __del__(self):
        os.remove(self.name)

def pack_hook(tensor):
    temp_file = SelfDeletingTempFile()
    torch.save(tensor, temp_file.name)
    return temp_file

def unpack_hook(temp_file):
    return torch.load(temp_file.name, weights_only=True)

当我们调用 backward 时，pack_hook 的输出将被删除，这会导致文件被删除，因此我们不再泄露文件。

然后这可以在您的模型中按以下方式使用

# Only save on disk tensors that have size >= 1000
SAVE_ON_DISK_THRESHOLD = 1000

def pack_hook(x):
    if x.numel() < SAVE_ON_DISK_THRESHOLD:
        return x
    temp_file = SelfDeletingTempFile()
    torch.save(tensor, temp_file.name)
    return temp_file

def unpack_hook(tensor_or_sctf):
    if isinstance(tensor_or_sctf, torch.Tensor):
        return tensor_or_sctf
    return torch.load(tensor_or_sctf.name)

class SaveToDisk(nn.Module):
    def __init__(self, module):
        super().__init__()
        self.module = module

    def forward(self, *args, **kwargs):
        with torch.autograd.graph.saved_tensors_hooks(pack_hook, unpack_hook):
            return self.module(*args, **kwargs)

net = nn.DataParallel(SaveToDisk(Model()))

在最后一个例子中，我们还演示了如何过滤应该保存哪些张量（这里指元素数量大于 1000 的张量），以及如何将此功能与 nn.DataParallel 结合。

如果您已经读到这里，恭喜您！您现在知道如何使用保存的张量钩子，以及它们在某些场景中如何有用，以权衡内存和计算。