torch.autograd 温和入门

创建日期：2017 年 3 月 24 日 | 最后更新日期：2025 年 1 月 10 日 | 最后验证日期：2024 年 11 月 5 日

torch.autograd 是 PyTorch 的自动微分引擎，为神经网络训练提供支持。在本节中，你将从概念上了解 autograd 如何帮助神经网络进行训练。

背景

神经网络（NNs）是一系列嵌套函数，对一些输入数据执行操作。这些函数由 *参数* (由权重和偏差组成) 定义，在 PyTorch 中，这些参数存储在张量中。

训练神经网络分两个步骤进行

前向传播：在前向传播中，神经网络对其正确输出做出最佳猜测。它将输入数据通过每个函数来做出这个猜测。

反向传播：在反向传播中，神经网络根据猜测的误差按比例调整其参数。它通过从输出向后遍历，收集误差对函数参数的导数（*梯度*），并使用梯度下降法优化参数来实现这一点。有关反向传播的更详细介绍，请观看 3Blue1Brown 的这个视频。

在 PyTorch 中的使用

让我们来看一个训练步骤。对于这个例子，我们从 torchvision 加载一个预训练的 resnet18 模型。我们创建一个随机数据张量来表示一个具有 3 个通道、高和宽都为 64 的单张图片，以及其对应的初始化为一些随机值的 label。在预训练模型中，标签的形状是 (1,1000)。

注意

本教程仅适用于 CPU，不适用于 GPU 设备（即使张量移动到 CUDA 上也不行）。

import torch
from torchvision.models import resnet18, ResNet18_Weights
model = resnet18(weights=ResNet18_Weights.DEFAULT)
data = torch.rand(1, 3, 64, 64)
labels = torch.rand(1, 1000)

Downloading: "https://download.pytorch.org/models/resnet18-f37072fd.pth" to /var/lib/ci-user/.cache/torch/hub/checkpoints/resnet18-f37072fd.pth

  0%|          | 0.00/44.7M [00:00<?, ?B/s]
 89%|########9 | 39.8M/44.7M [00:00<00:00, 417MB/s]
100%|##########| 44.7M/44.7M [00:00<00:00, 418MB/s]

接下来，我们将输入数据通过模型的每个层运行，以进行预测。这就是前向传播 (forward pass)。

prediction = model(data) # forward pass

我们使用模型的预测结果和相应的标签来计算误差 (loss)。下一步是将这个误差通过网络反向传播。当我们对误差张量调用 .backward() 时，反向传播就开始了。然后，Autograd 会计算并存储每个模型参数的梯度，保存在参数的 .grad 属性中。

loss = (prediction - labels).sum()
loss.backward() # backward pass

接下来，我们加载一个优化器，在本例中是学习率为 0.01、动量为 0.9 的 SGD。我们将模型的所有参数注册到优化器中。

optim = torch.optim.SGD(model.parameters(), lr=1e-2, momentum=0.9)

最后，我们调用 .step() 来启动梯度下降。优化器根据存储在 .grad 中的梯度调整每个参数。

optim.step() #gradient descent

至此，你已经具备了训练神经网络所需的一切。以下部分详细介绍了 autograd 的工作原理——你可以自由选择是否跳过。

---

Autograd 中的微分

让我们看看 autograd 如何收集梯度。我们创建两个张量 a 和 b，并将 requires_grad 标志设置为 True。这会向 autograd 发出信号，表明对它们进行的每个操作都应该被跟踪。

import torch

a = torch.tensor([2., 3.], requires_grad=True)
b = torch.tensor([6., 4.], requires_grad=True)

我们从 a 和 b 创建另一个张量 Q。

\[Q = 3a^3 - b^2 \]

Q = 3*a**3 - b**2

假设 a 和 b 是神经网络的参数，而 Q 是误差。在神经网络训练中，我们想要误差相对于参数的梯度，即：

\[\frac{\partial Q}{\partial a} = 9a^2 \]

\[\frac{\partial Q}{\partial b} = -2b \]

当我们对 Q 调用 .backward() 时，autograd 会计算这些梯度并将其存储在相应张量的 .grad 属性中。

我们需要在 Q.backward() 中明确传递一个 gradient 参数，因为 Q 是一个向量。gradient 是一个与 Q 形状相同的张量，它表示 Q 对自身的梯度，即：

\[\frac{dQ}{dQ} = 1 \]

同样地，我们也可以将 Q 聚合成一个标量，并隐式地调用 backward，例如 Q.sum().backward()。

external_grad = torch.tensor([1., 1.])
Q.backward(gradient=external_grad)

梯度现在已存入 a.grad 和 b.grad 中

# check if collected gradients are correct
print(9*a**2 == a.grad)
print(-2*b == b.grad)

tensor([True, True])
tensor([True, True])

拓展阅读 - 使用 autograd 进行向量微积分

从数学上讲，如果有一个向量值函数 \(\vec{y}=f(\vec{x})\)，则 \(\vec{y}\) 关于 \(\vec{x}\) 的梯度是一个雅可比矩阵 \(J\)

\[J = \left(\begin{array}{cc} \frac{\partial \bf{y}}{\partial x_{1}} & ... & \frac{\partial \bf{y}}{\partial x_{n}} \end{array}\right) = \left(\begin{array}{ccc} \frac{\partial y_{1}}{\partial x_{1}} & \cdots & \frac{\partial y_{1}}{\partial x_{n}}\\ \vdots & \ddots & \vdots\\ \frac{\partial y_{m}}{\partial x_{1}} & \cdots & \frac{\partial y_{m}}{\partial x_{n}} \end{array}\right)\]

一般来说，torch.autograd 是一个计算向量-雅可比积的引擎。也就是说，给定任意向量 \(\vec{v}\)，计算乘积 \(J^{T}\cdot \vec{v}\)

如果 \(\vec{v}\) 恰好是标量函数 \(l=g\left(\vec{y}\right)\) 的梯度

\[\vec{v} = \left(\begin{array}{ccc}\frac{\partial l}{\partial y_{1}} & \cdots & \frac{\partial l}{\partial y_{m}}\end{array}\right)^{T}\]

那么根据链式法则，向量-雅可比积将是 \(l\) 关于 \(\vec{x}\) 的梯度

\[J^{T}\cdot \vec{v} = \left(\begin{array}{ccc} \frac{\partial y_{1}}{\partial x_{1}} & \cdots & \frac{\partial y_{m}}{\partial x_{1}}\\ \vdots & \ddots & \vdots\\ \frac{\partial y_{1}}{\partial x_{n}} & \cdots & \frac{\partial y_{m}}{\partial x_{n}} \end{array}\right)\left(\begin{array}{c} \frac{\partial l}{\partial y_{1}}\\ \vdots\\ \frac{\partial l}{\partial y_{m}} \end{array}\right) = \left(\begin{array}{c} \frac{\partial l}{\partial x_{1}}\\ \vdots\\ \frac{\partial l}{\partial x_{n}} \end{array}\right)\]

向量-雅可比积的这一特性正是我们在上述示例中使用的；external_grad 表示 \(\vec{v}\)。

计算图

从概念上讲，autograd 在一个由 Function 对象组成的有向无环图（DAG）中记录数据（张量）以及所有执行的操作（以及由此产生的新张量）。在这个 DAG 中，叶子是输入张量，根是输出张量。通过从根到叶追溯这个图，你可以使用链式法则自动计算梯度。

在前向传播中，autograd 同时做两件事

• 运行请求的操作以计算结果张量，以及

• 在 DAG 中维护操作的 *梯度函数*。

当在 DAG 根节点上调用 .backward() 时，反向传播开始。autograd 接着

• 从每个 .grad_fn 计算梯度，

• 将它们累积到相应张量的 .grad 属性中，并且

• 使用链式法则，一直传播到叶子张量。

下图是示例中 DAG 的可视化表示。在图中，箭头指向前向传播的方向。节点代表前向传播中每个操作的反向函数。蓝色的叶子节点代表我们的叶子张量 a 和 b。

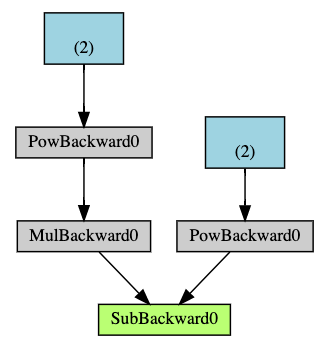
注意

PyTorch 中的 DAG 是动态的 需要注意的一点是，图是每次从头开始重新创建的；在每次调用 .backward() 后，autograd 开始填充一个新的图。这正是允许你在模型中使用控制流语句的原因；如果需要，你可以在每次迭代时改变形状、大小和操作。

从 DAG 中排除

torch.autograd 会跟踪所有将 requires_grad 标志设置为 True 的张量上的操作。对于不需要梯度的张量，将其此属性设置为 False 会将其从梯度计算 DAG 中排除。

即使只有一个输入张量将 requires_grad 设置为 True，操作的输出张量也将需要梯度。

x = torch.rand(5, 5)
y = torch.rand(5, 5)
z = torch.rand((5, 5), requires_grad=True)

a = x + y
print(f"Does `a` require gradients?: {a.requires_grad}")
b = x + z
print(f"Does `b` require gradients?: {b.requires_grad}")

Does `a` require gradients?: False
Does `b` require gradients?: True

在神经网络中，不计算梯度的参数通常称为冻结参数。如果你事先知道不需要某些参数的梯度，那么“冻结”模型的一部分会很有用（这可以通过减少 autograd 计算来提供一些性能优势）。

在微调中，我们冻结模型的大部分，通常只修改分类器层以对新标签进行预测。让我们来看一个小例子来演示这一点。像之前一样，我们加载一个预训练的 resnet18 模型，并冻结所有参数。

from torch import nn, optim

model = resnet18(weights=ResNet18_Weights.DEFAULT)

# Freeze all the parameters in the network
for param in model.parameters():
    param.requires_grad = False

假设我们想在一个包含 10 个新标签的数据集上微调模型。在 resnet 中，分类器是最后一个线性层 model.fc。我们可以简单地用一个新的线性层（默认不冻结）替换它，作为我们的分类器。

model.fc = nn.Linear(512, 10)

现在模型中除了 model.fc 的参数外，所有参数都已冻结。唯一计算梯度的参数是 model.fc 的权重和偏差。

# Optimize only the classifier
optimizer = optim.SGD(model.parameters(), lr=1e-2, momentum=0.9)

注意，尽管我们在优化器中注册了所有参数，但唯一计算梯度（并因此在梯度下降中更新）的参数是分类器的权重和偏差。

同样的排除功能也可以通过上下文管理器 torch.no_grad() 使用

---

延伸阅读：

• 就地操作与多线程 Autograd

• 反向模式自动微分示例实现

• 视频：PyTorch Autograd 解释 - 深入教程