PyTorch Autograd 引擎概述 – PyTorch

本博文基于 PyTorch 1.8 版本，但也适用于较旧的版本，因为大部分机制保持不变。

为了帮助理解此处解释的概念，如果您不熟悉 PyTorch 架构组件（如 ATen 或 c10d），建议您阅读 @ezyang 的精彩博文：PyTorch 内部原理。

什么是 autograd？

背景

PyTorch 使用自动微分来计算函数相对于输入的梯度。自动微分是一种技术，给定一个计算图，它可以计算输入的梯度。自动微分可以通过两种不同的方式执行：前向模式和反向模式。前向模式意味着我们同时计算梯度和函数结果，而反向模式要求我们首先评估函数，然后从输出开始计算梯度。虽然两种模式都有其优缺点，但反向模式是事实上的选择，因为输出的数量少于输入的数量，这使得计算效率更高。请参阅 [3] 了解更多信息。

自动微分依赖于经典微积分公式，即链式法则。链式法则允许我们通过分解和重组来计算非常复杂的导数。

形式上，给定一个复合函数 $f(g(x))$ ，我们可以将其导数计算为 $\frac{\partial}{\partial x} f(g(x)) = f'(g(x))g'(x)$ 。这个结果是自动微分工作的基础。通过组合构成一个更大函数（例如神经网络）的简单函数的导数，可以计算给定点的梯度的精确值，而不是依赖数值近似，后者需要对输入进行多次扰动才能获得一个值。

为了直观地了解反向模式的工作原理，让我们看一个简单的函数 $f(x, y) = log(x*y)$ 。图 1 显示了其计算图，其中左侧的输入 x、y 流经一系列操作以生成输出 z。

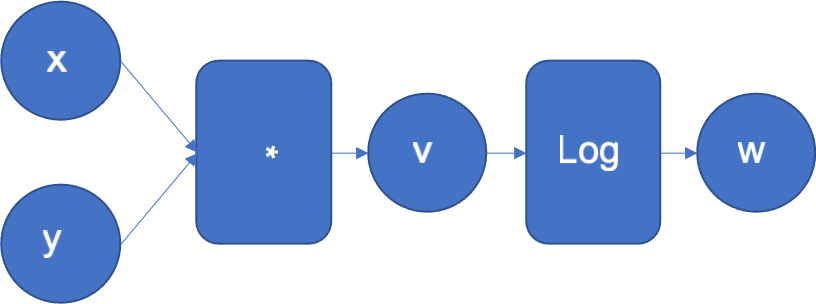
图 1：f(x, y) = log(x*y) 的计算图

自动微分引擎通常会执行此图。它还会扩展此图以计算 w 相对于输入 x、y 和中间结果 v 的导数。

示例函数可以分解为 f 和 g，其中 $f(x, y) = log(g(x, y))$ 和 $g(x, y) = xy$ 。每当引擎执行图中的操作时，该操作的导数就会添加到图中，以便稍后在反向传播中执行。请注意，引擎知道基本函数的导数。

在上面的示例中，当 x 和 y 相乘得到 v 时，引擎将扩展图以使用它已经知道的乘法导数定义来计算乘法的偏导数。 $\frac{\partial}{\partial x} g(x, y) = y$ 和 $\frac{\partial}{\partial y} g(x, y) = x$ 。生成的扩展图如图 2 所示，其中 *MultDerivative* 节点还通过输入梯度计算所得梯度的乘积以应用链式法则；这将在以下操作中明确体现。请注意，反向图（绿色节点）在所有前向步骤完成之前不会执行。

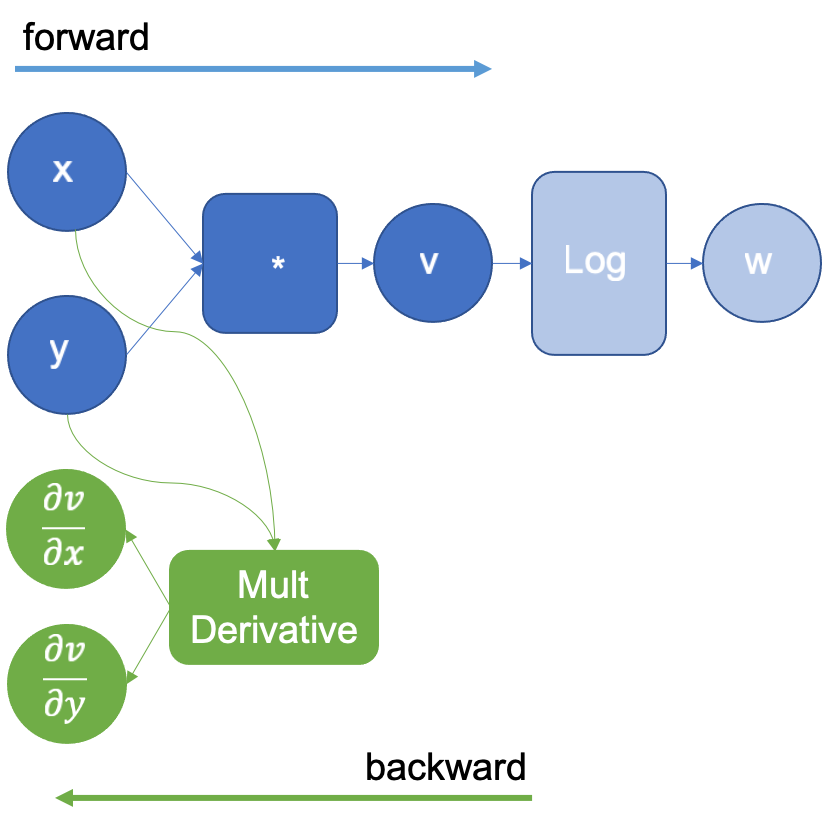
图 2：执行对数后扩展的计算图

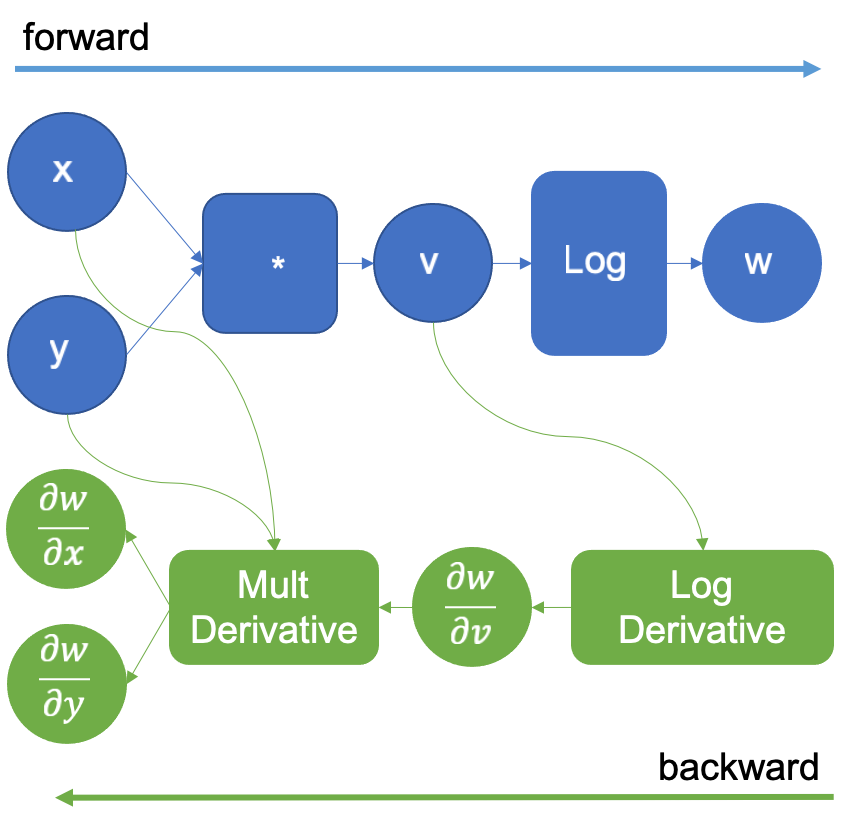
接着，引擎现在计算 $log(v)$ 操作，并再次使用它知道的对数导数（即 $\frac{1}{v}$ ）来扩展图。如图 3 所示。此操作生成结果 $\frac{\partial w}{\partial v}$ ，当它反向传播并乘以乘法导数（如链式法则所示）时，生成导数 $\frac{\partial w}{\partial x}$ 、 $\frac{\partial w}{\partial y}$ 。

图 3：执行对数后扩展的计算图

原始计算图通过一个新的虚拟变量 z 进行扩展，z 与 w 相同。z 相对于 w 的导数是 1，因为它们是相同的变量，这个技巧允许我们应用链式法则来计算输入的导数。在前向传播完成后，我们通过提供 $\frac{\partial z}{\partial w}$ 的初始值 1.0 来开始反向传播。如图 4 所示。

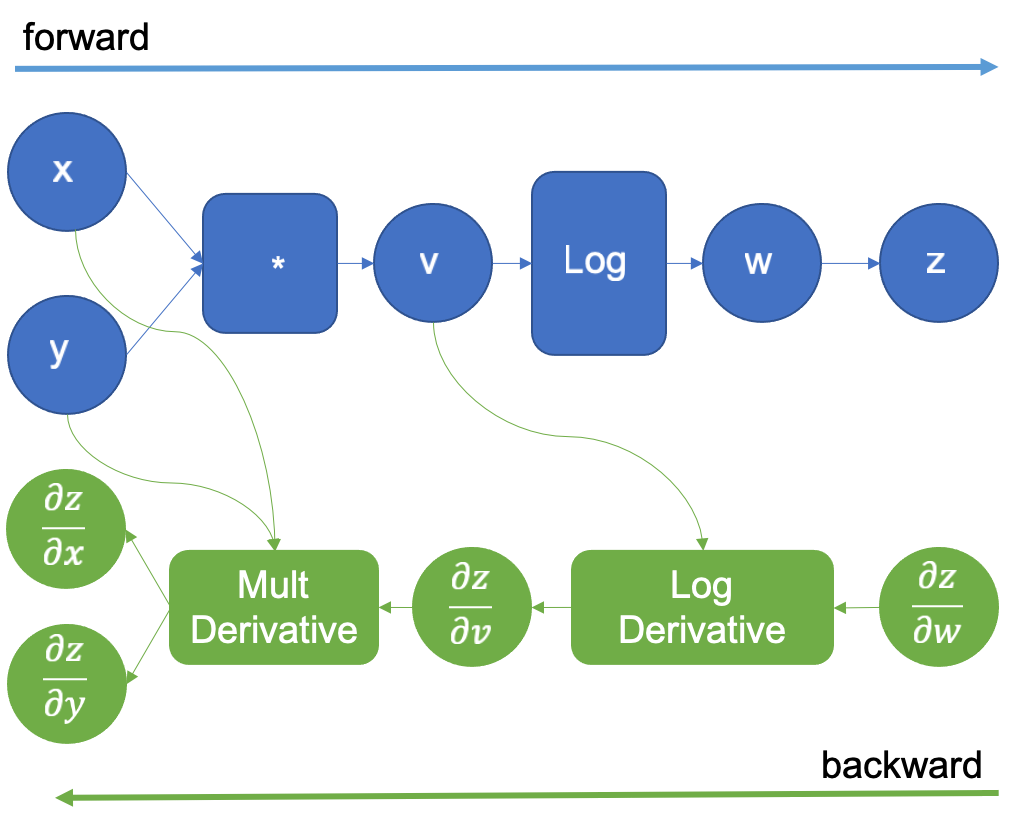
图 4：为反向自动微分扩展的计算图

然后沿着绿色图执行自动微分引擎引入的 LogDerivative 操作 $\frac{1}{v}$ ，并将其结果乘以 $\frac{\partial z}{\partial w}$ ，以根据链式法则获得梯度 $\frac{\partial z}{\partial v}$ 。接下来，以相同的方式执行乘法导数，并最终获得所需的导数 $\frac{\partial z}{\partial x} \frac{\partial z}{\partial y}$ 。

形式上，我们在这里所做的以及 PyTorch autograd 引擎所做的，是计算雅可比向量积 (Jvp) 以计算模型参数的梯度，因为模型参数和输入是向量。

雅可比向量积

当我们计算向量值函数 $f(\overline{x}) = \overline{y}$ （其输入和输出都是向量的函数）的梯度时，我们本质上是在构建一个雅可比矩阵。

由于链式法则，将函数 $f(\overline{x}) = \overline{y}$ 的雅可比矩阵乘以一个向量 $v$ （其中 $v$ 包含标量函数 $z = g(\overline{y})$ 之前计算的梯度），会得到标量输出相对于向量值函数输入的梯度 $\frac{\partial z}{\partial x_1} \cdots \frac{\partial z}{\partial x_n}$ 。

举个例子，让我们看看一些用 Python 符号表示的函数，以展示链式法则如何应用。


      def f(x1, x2):
      a = x1 * x2
      y1 = log(a)
      y2 = sin(x2)
      return (y1, y2)

  def g(y1, y2):
      return y1 * y2

现在，如果我们手工使用链式法则和导数定义进行推导，我们将获得以下一组恒等式，我们可以将其直接插入到 $f(x_1, x_2)$ 的雅可比矩阵中。

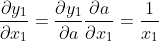
$\frac{\partial y_1}{\partial x_1} = \frac{\partial y_1}{\partial a}\frac{\partial a}{\partial x_1} = \frac{1}{x_1}$

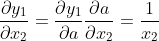
$\frac{\partial y_1}{\partial x_2} = \frac{\partial y_1}{\partial a}\frac{\partial a}{\partial x_2} = \frac{1}{x_2}$

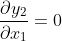
$\frac{\partial y_2}{\partial x_1} = 0$

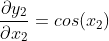
$\frac{\partial y_2}{\partial x_2} = cos(x_2)$

接下来，让我们考虑标量函数 $z = g(y_1, y_2)$ 的梯度

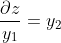
$\frac{\partial z}{y_1} = y_2$

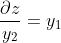
$\frac{\partial z}{y_2} = y_1$

如果现在我们计算遵循链式法则的转置雅可比向量积，我们得到以下表达式

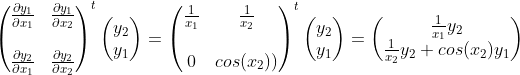
\begin{pmatrix}\frac{\partial y_1}{\partial x_1} & \frac{\partial y_1}{\partial x_2} \\\\ \frac{\partial y_2}{\partial x_1} & \frac{\partial y_2}{\partial x_2} \end{pmatrix}^{t} \begin{pmatrix} y_2\\y_1 \end{pmatrix} = \begin{pmatrix}\frac{1}{x_1} & \frac{1}{x_2} \\\\ 0 & cos(x_2)) \end{pmatrix}^{t} \begin{pmatrix} y_2\\y_1 \end{pmatrix} = \begin{pmatrix} \frac{1}{x_1}y_2\\\frac{1}{x_2}y_2+cos(x_2)y_1 \end{pmatrix}

对 $(x_1, x_2) = (0.5, 0.75)$ 评估 Jvp 得到结果： $(\frac{dy}{x_1}, \frac{dy}{x_2}) = (1.3633, 0.1912)$ 我们可以 PyTorch 中执行相同的表达式并计算输入的梯度

>>> import torch
>>> x = torch.tensor([0.5, 0.75], requires_grad=True)
>>> y = torch.log(x[0] * x[1]) * torch.sin(x[1])
>>> y.backward(1.0)
>>> x.grad
tensor([1.3633, 0.1912])

结果与我们手动计算的雅可比向量积相同！然而，PyTorch 从未构造矩阵，因为它可能变得非常大，而是创建了一个操作图，该图在反向遍历时应用了 tools/autograd/derivatives.yaml 中定义的雅可比向量积。

遍历图

每次 PyTorch 执行一个操作时，autograd 引擎都会构建一个用于反向遍历的图。反向模式自动微分通过在末尾添加一个标量变量 $z = w$ 来启动，这样 $\frac{\partial z}{\partial w} = 1$ ，正如我们在介绍中看到的。这是在 Jvp 引擎计算中提供的初始梯度值，正如我们在上一节中看到的。

在 PyTorch 中，用户在调用 backward 方法时明确设置了初始梯度。

然后，Jvp 计算开始，但它从不构建矩阵。相反，当 PyTorch 记录计算图时，执行的前向操作的导数被添加（反向节点）。图 5 显示了由之前看到的函数 $f(x_1, x_2)$ 和 $g(y_1, y_2)$ 的执行生成的反向图。

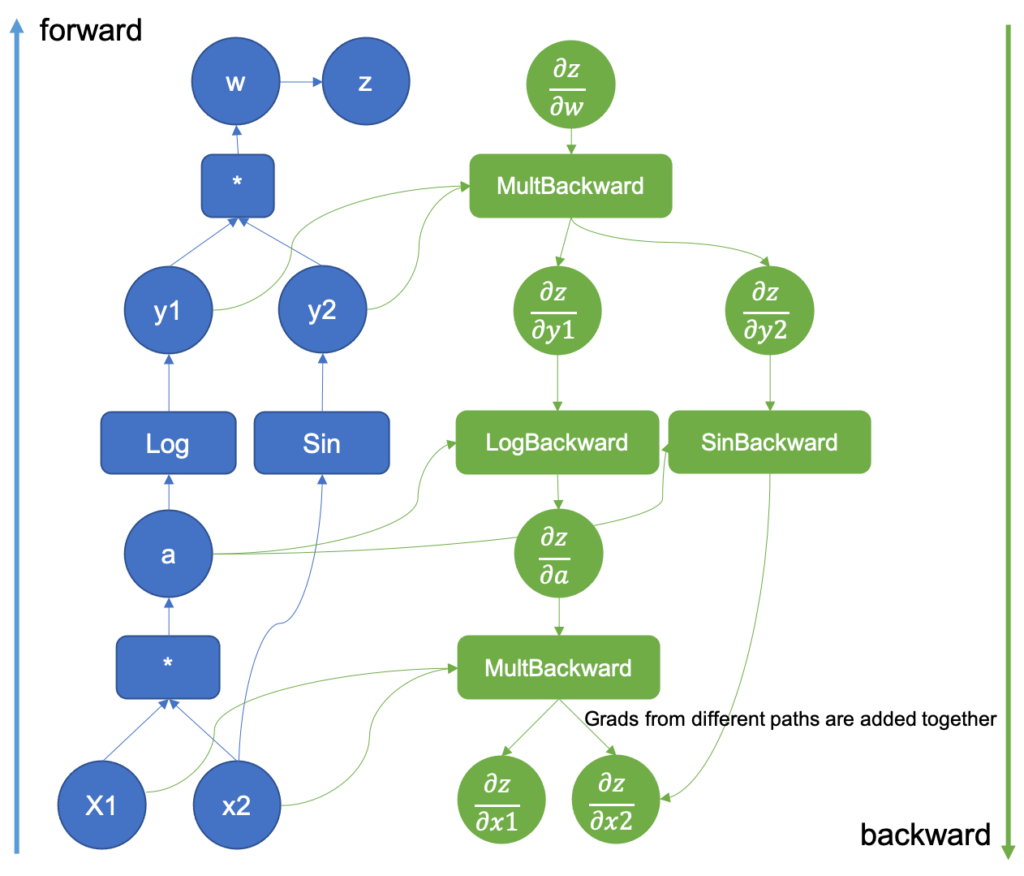
图 5：扩展了反向传播的计算图

前向传播完成后，结果将在反向传播中使用，其中计算图中的导数被执行。基本导数存储在 tools/autograd/derivatives.yaml 文件中，它们不是常规导数，而是它们的 Jvp 版本 [3]。它们将原始函数的输入和输出作为参数，以及函数输出相对于最终输出的梯度。通过重复将结果梯度乘以图中下一个 Jvp 导数，将按照链式法则生成直到输入的梯度。

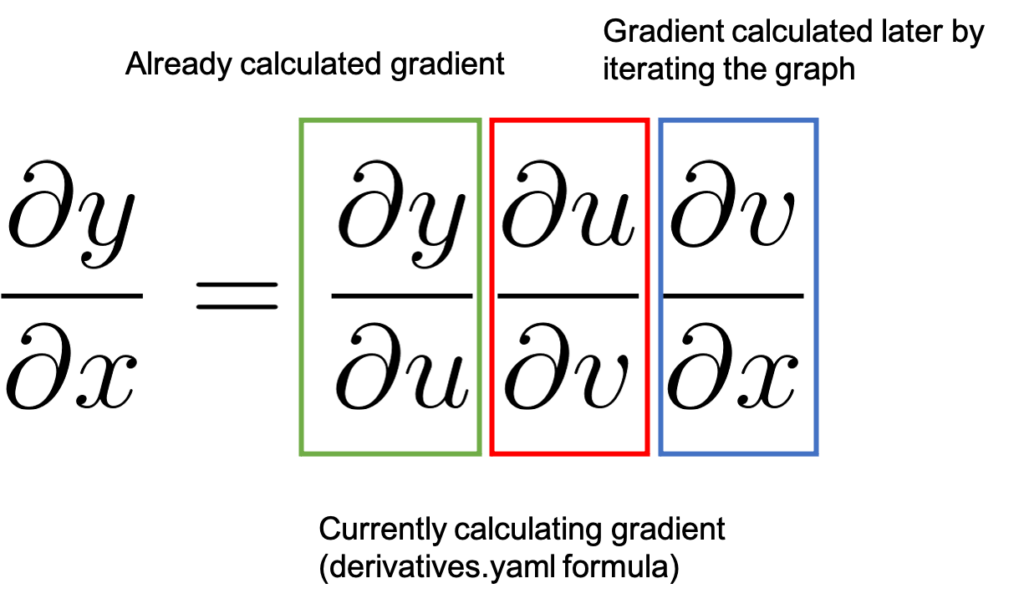
图 6：链式法则在反向微分中的应用方式

图 6 通过展示链式法则来表示该过程。我们从 1.0 的值开始，如前所述，这是已经计算出的梯度 $\frac{\partial y}{\partial u}$ ，以绿色突出显示。然后我们移动到图中的下一个节点。在 derivatives.yaml 中注册的 *backward* 函数将计算相关的 $\frac{\partial u}{\partial v}$ 值，以红色突出显示，并将其乘以 $\frac{\partial y}{\partial u}$ 。根据链式法则，这会得到 $\frac{\partial y}{\partial v}$ ，这将是我们处理图中下一个反向节点时已经计算出的梯度（绿色）。

您可能还注意到，在图 5 中，有一个梯度来自两个不同的来源。当两个不同的函数共享一个输入时，相对于输出的梯度会聚合到该输入，并且只有当所有路径都聚合在一起时，才能继续使用该梯度进行计算。

让我们看一个 PyTorch 中如何存储导数的示例。

假设我们正在处理图 2 中 *LogBackward* 节点中的 $log$ 函数的反向传播。在 derivatives.yaml 中， $log$ 的导数指定为 grad.div(self.conj())。grad 是已经计算出的梯度 $\frac{\partial z}{\partial y1}$ ，而 self.conj() 是输入向量的复共轭。对于复数，PyTorch 计算一个特殊的导数，称为共轭 Wirtinger 导数 [6]。这个导数接受复数及其共轭，并通过 [6] 中描述的一些神奇操作，当它们插入优化器时，它们就是最陡下降的方向。

此代码转换为 $(\frac{\partial z}{\partial y1} \frac{1}{v})$ ，即图 3 中对应的绿色和红色方块。接下来，autograd 引擎将执行下一个操作：乘法的反向传播。与以前一样，输入是原始函数的输入以及从 $log$ 反向传播步骤计算出的梯度。此步骤将重复进行，直到我们到达相对于输入的梯度，计算将完成。只有当乘法和 sin 梯度相加后， $\frac{\partial z}{x2}$ 的梯度才算完成。如您所见，我们计算了与 Jvp 等效的结果，但没有构建矩阵。

在下一篇文章中，我们将深入研究 PyTorch 代码，看看这个图是如何构建的，以及如果您想尝试它，相关的部分在哪里！

PyTorch 自动微分引擎概述

什么是 autograd？

参考文献

文档

教程

资源

保持联系以获取更新、活动信息和最新新闻