IBM:Krish Agarwal, Rishi Astra, Adnan Hoque, Mudhakar Srivatsa, Raghu Ganti
Meta:Less Wright, Sijia Chen
量化是一种通过压缩模型权重并在较低精度数据类型中执行(更快速的)计算来提高模型推理速度的方法。然而,量化可能会因异常值的存在而导致精度损失。最近的工作,如QuaRot、SpinQuant和FlashAttention-3,引入了提高LLM中INT4、INT8和FP8量化数值精度的方法。这些方法依赖于Hadamard变换。在本博客中,我们介绍了HadaCore,一个Hadamard变换CUDA内核,它在NVIDIA A100和H100 GPU上实现了最先进的性能。我们的内核相对于Dao AI Lab的快速Hadamard变换内核,速度提升了1.1-1.4倍和1.0-1.3倍,峰值增益分别为3.5倍和3.6倍。我们利用了硬件感知的任务分解,在保持量化误差降低的同时,受益于Tensor Core加速。
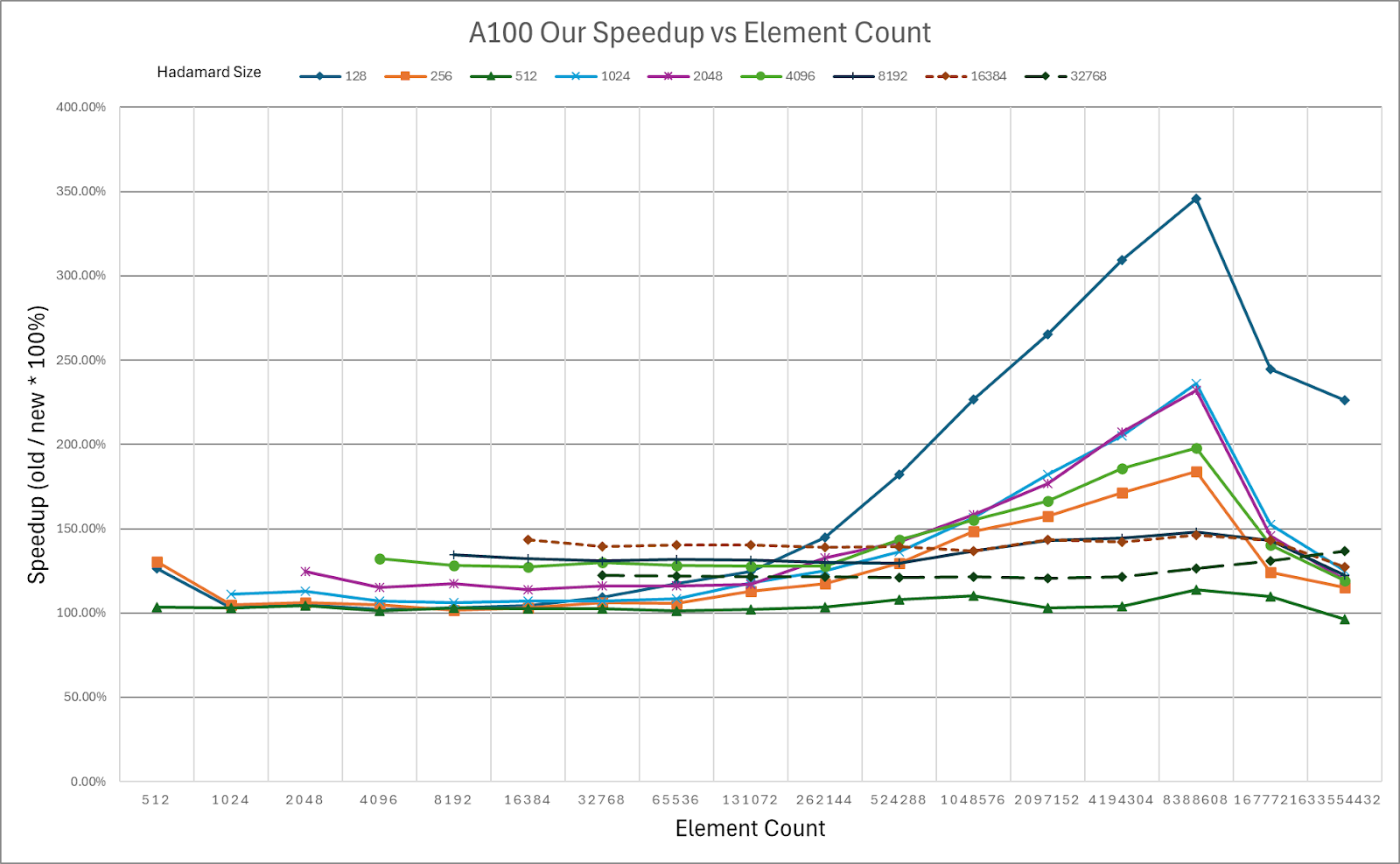
图1:HadaCore与Dao AI Hadamard CUDA内核的速度提升。在A100上,通过对8.4M元素进行128次旋转,实现了3.46倍的峰值增益。
背景
QuaRot和SpinQuant都提出了提高LLM中INT4和INT8量化数值精度的方法。这两种方法都旋转模型激活,因为从统计学上讲,旋转可以减少异常值的幅度,因为它将极端值“分散”到其他(不那么极端)的维度中,而且旋转也是一种易于使用旋转矩阵的逆矩阵进行可逆的操作。这些方法还可以提高FP8推理精度,例如在FlashAttention-3中。
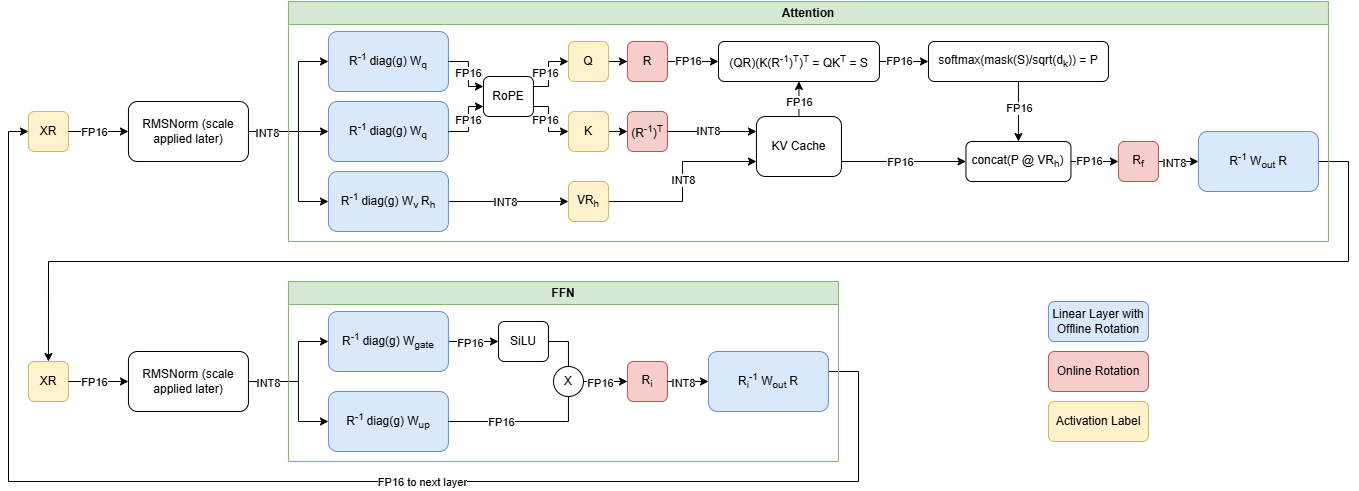
图2:Transformer块,显示QuaRot中的在线(红色)和离线(蓝色)旋转。
应用这些旋转矩阵会引入模型运行时开销,如图2所示的在线操作。这些旋转可以通过矩阵乘法应用,但增加的开销会削弱量化带来的好处。因此,QuaRot和SpinQuant选择使用Walsh-Hadamard矩阵,这是一种特殊类型的旋转矩阵,可以使用快速Walsh-Hadamard变换算法比矩阵乘法更快地应用。HadaCore是该算法针对支持Tensor Cores的NVIDIA GPU的优化实现。
Tensor Core加速的Hadamard变换
HadaCore利用了NVIDIA Tensor Cores,它们是NVIDIA GPU上专门用于矩阵乘法的计算单元。为了实现这一点,我们的内核对快速Walsh-Hadamard算法进行了硬件感知的任务分解。这种任务分解确保我们能够利用在Tensor Core芯片上执行的MMA PTX指令。HadaCore对输入数据的块应用16×16 Hadamard变换。然后,计算可以卸载到FP16 Tensor Core,并使用mma.m16n8k16指令。HadaCore的warp级并行化如下所示。

图3:HadaCore并行化,1×256向量(行)通过大小为256的Hadamard进行旋转。
我们使用warp级Tensor Core操作并行处理256个元素的片段,以实现最大256大小的Hadamard变换。对于更大的尺寸,我们在warp之间进行数据混洗并重复。
微基准测试
我们使用NVIDIA H100和A100 GPU,在不同的Hadamard和输入张量大小下,对HadaCore与Dao AI Lab Hadamard内核进行了基准测试。
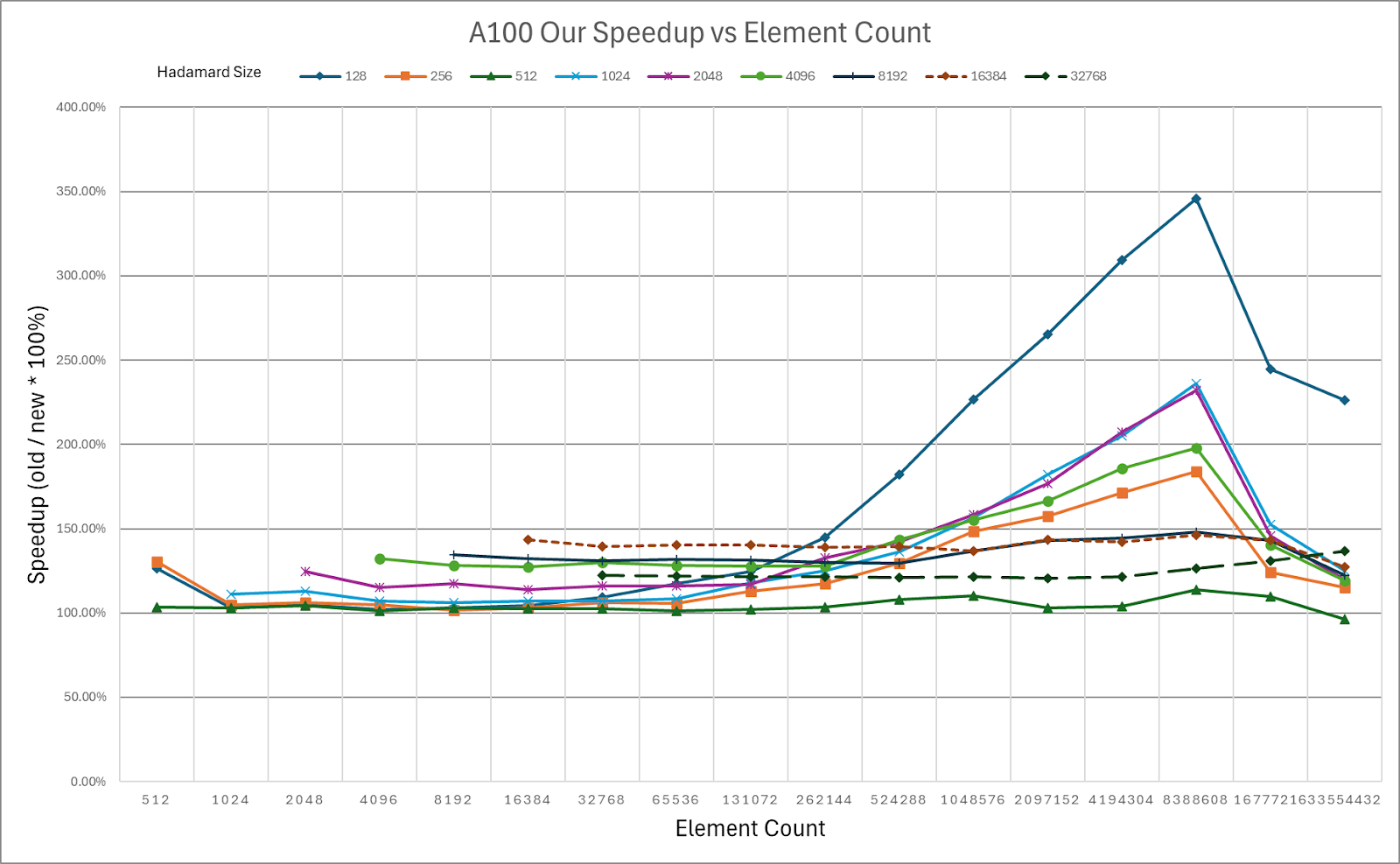
图4:HadaCore内核在NVIDIA A100上相对于Dao AI Lab快速Hadamard内核的速度提升。

NVIDIA A100的速度提升彩色编码表,绿色 = 相对于基线的速度提升。
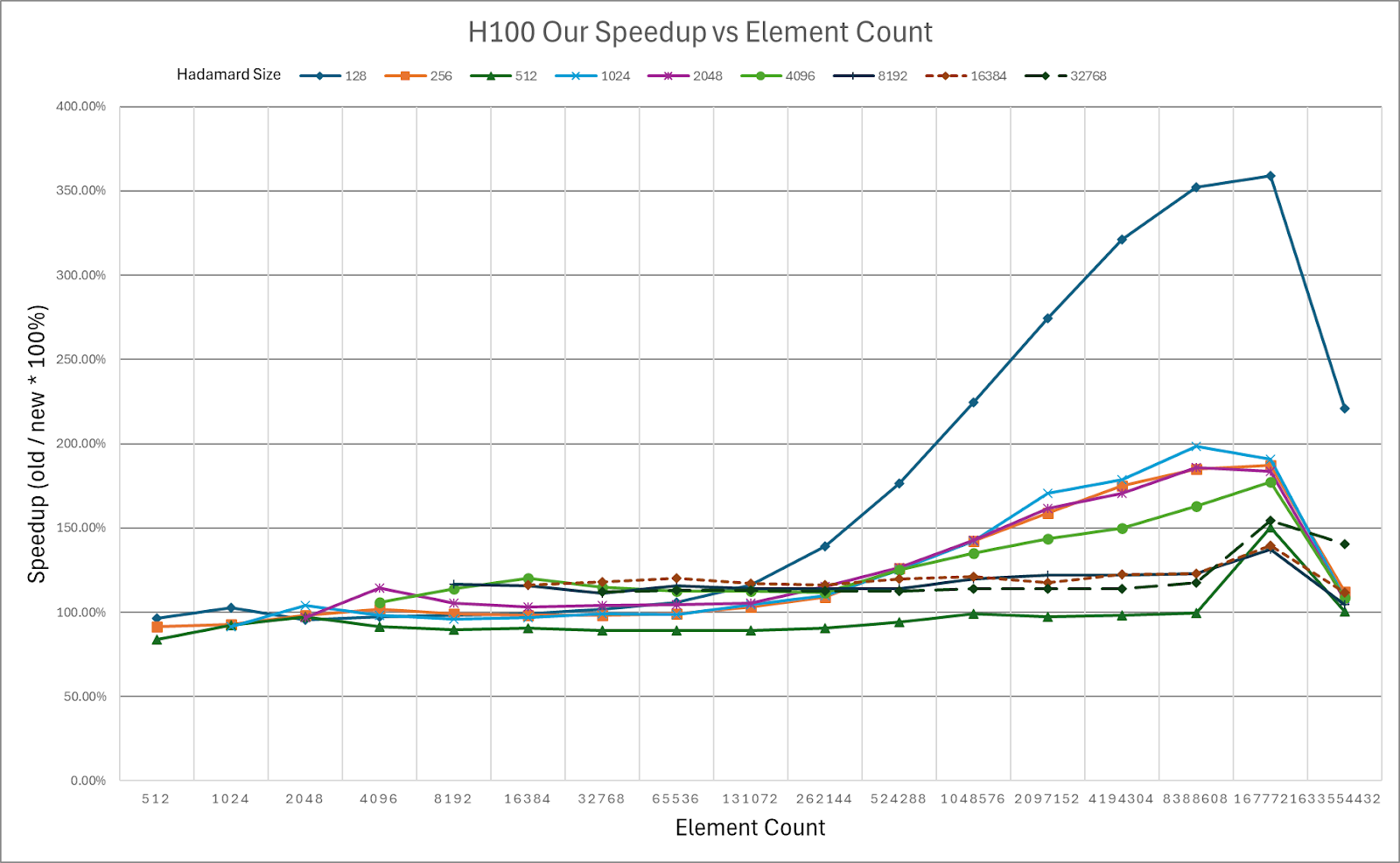
图5:HadaCore内核在NVIDIA H100上相对于Dao AI Lab快速Hadamard内核的速度提升。

NVIDIA H100的速度提升彩色编码表,绿色 = 相对于基线的速度提升。
我们的图表显示,随着输入张量大小(标记为元素计数)的增加,我们的速度提升也随之增加。元素计数是我们正在旋转的目标矩阵中的元素数量。例如,在多头注意力中
查询(Q)、键(K)和值(V)张量是大小为
(batch_size,seq_len,n_heads,head_dim)
的4D张量。Hadamard矩阵的大小为head_dim,应用于这些激活张量,因此我们称之为使用head_dim的Hadamard大小,元素计数为
batch_size * seq_len * n_heads * head_dim。
注意力块中查询旋转的常见元素计数
| 模型 \ Tokens | 预填充 | 解码 |
| Llama-2 70b | 33,554,432个元素 128 Hadamard尺寸 (1批次 * 64个头 * 4096个tokens * 每个头每个token 128维嵌入) |
8192个元素 128 Hadamard尺寸 (1批次 * 64个头 * 1个token * 每个头每个token 128维嵌入) |
| Llama-3 8b | 33,554,432个元素 128 Hadamard尺寸 (1批次 * 32个头 * 8192个tokens * 每个头每个token 128维嵌入) |
4,096个元素 128 Hadamard尺寸 (1批次 * 32个头 * 1个token * 每个头每个token 128维嵌入) |
HadaCore在A100上相对于Dao AI Lab的快速Hadamard内核,速度提升了1.1-1.4倍,在H100上速度提升了1.0-1.3倍,峰值增益分别为3.5倍和3.6倍。对于H100上的较小尺寸,HadaCore的增益有所下降。对于未来的工作,我们计划结合使用Hopper特定的功能,如TMA和WGMMA,以提高H100的性能。
MMLU基准测试
我们评估了在FP8中执行FlashAttention计算的Llama 3.1-8B推理工作负载上的MMLU分数。新一代NVIDIA Hopper GPU配备了FP8 Tensor Cores,与FP16相比,它们提供了显著的计算增益。
我们的结果显示,HadaCore与FP8 FlashAttention等优化结合使用时,在保持精度方面的优势。
| 格式 | 方法 | Llama3.1-8B 平均5次MMLU准确度 |
| Q, K, V: FP16 FlashAttention: FP16 |
不适用 | 65.38 |
| Q, K, V: FP16 FlashAttention: FP8 |
无Hadamard | 64.40 |
| Q, K, V: FP8 FlashAttention: FP8 |
HadaCore | 65.09 |
| Q, K, V: FP8 FlashAttention: FP8 |
Dao AI快速Hadamard内核 | 65.45 |
表1:Llama3.1 8B的MMLU分数,采用FP16基线和使用Hadamard变换的FP8注意力,比较了使用显式Hadamard矩阵乘法与HadaCore的实现(越高越好)
从上述MMLU分数中,我们注意到对于使用FP8注意力的Llama3.1-8B推理,HadaCore改进了在较低精度下计算注意力引入的量化误差。
结论
我们展示了通过将快速Walsh-Hadamard算法移植到利用Tensor Core加速的CUDA内核所实现的速度提升,在NVIDIA A100和H100上,相对于Dao AI快速Hadamard内核,分别实现了3.5倍和3.6倍的峰值速度提升。
此外,我们在MMLU基准测试中表明,使用HadaCore进行旋转在计算加速的同时,保持了与快速Hadamard内核相似的量化误差降低。
未来工作
我们计划实现我们内核的Triton版本,并尝试更先进的技术,如内核融合以支持融合Hadamard变换和量化。此外,我们计划扩展我们的内核以支持BF16 Tensor Core计算。