在这篇博客文章中,我们探讨了论文 “快速而简洁:Triton 中的 2-单纯注意力” [1] 中提出的内核设计细节。我们首先用硬件对齐的设计对 2-单纯注意力算法进行建模,然后使用现代 GPU 内核技术,在 TLX (Triton Low-Level Extensions) [2] 中完全重写了整个内核。利用 TLX,我们成功地在 NVIDIA H100 GPU 上实现了 2-单纯注意力前向传播中高达 588 Tensor Core BF16 TFLOPs,大约 60% 的 Tensor Core 利用率,这比原始 Triton 内核的 337 峰值 TFLOPs 提升了约 1.74 倍的速度。
代码库:https://github.com/pytorch/FBGEMM/tree/main/fbgemm_gpu/experimental/simplicial_attention
† 在 Meta 工作期间完成
2-单纯注意力回顾
随着大型语言模型的不断扩展,获取足够高质量的训练词元变得越来越具有挑战性。提高注意力机制的词元效率对于解决这个问题至关重要。一个很有前途的进展是 2-单纯注意力(算法 1),它使用三线性函数来建模查询与两组键(K1、K2)和两组值(V1、V2)之间的交互,以建模词元三元组之间复杂的交互,而不是像标准点积注意力那样只建模词元对。正如论文《逻辑与 2-单纯 Transformer》[3] 中首次提出的那样,2-单纯注意力在基本保持原始模型大小的同时增加了注意力的 TFLOPs。根据缩放律实验,2-单纯注意力在词元效率方面显示出显著改进,特别是在数学和逻辑问题解决等推理任务中。

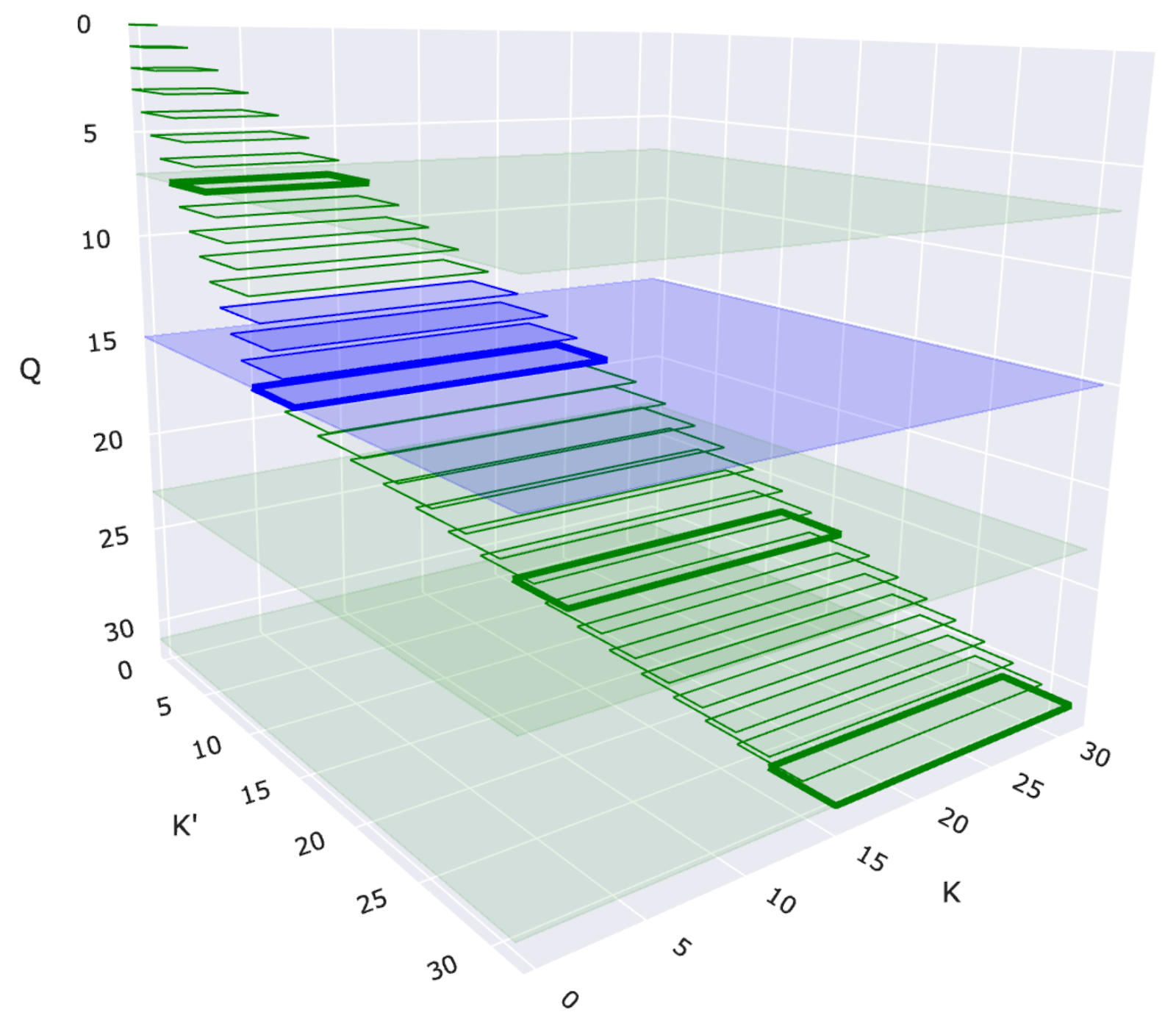
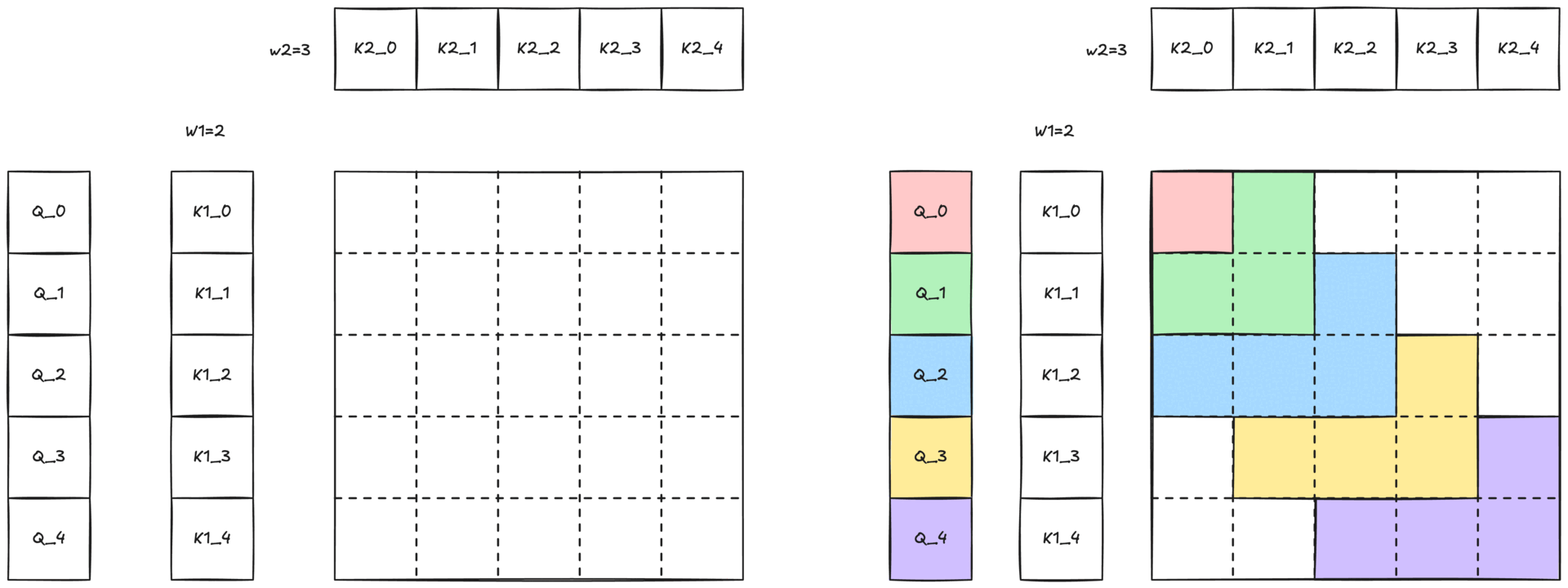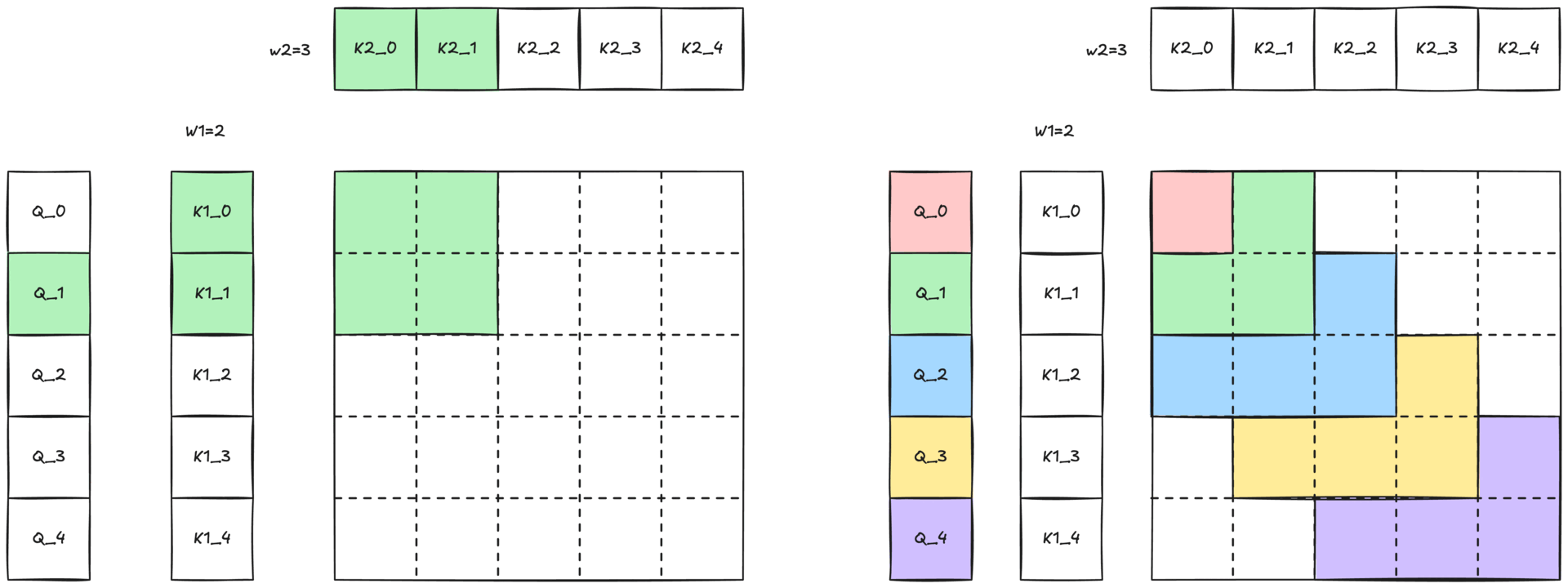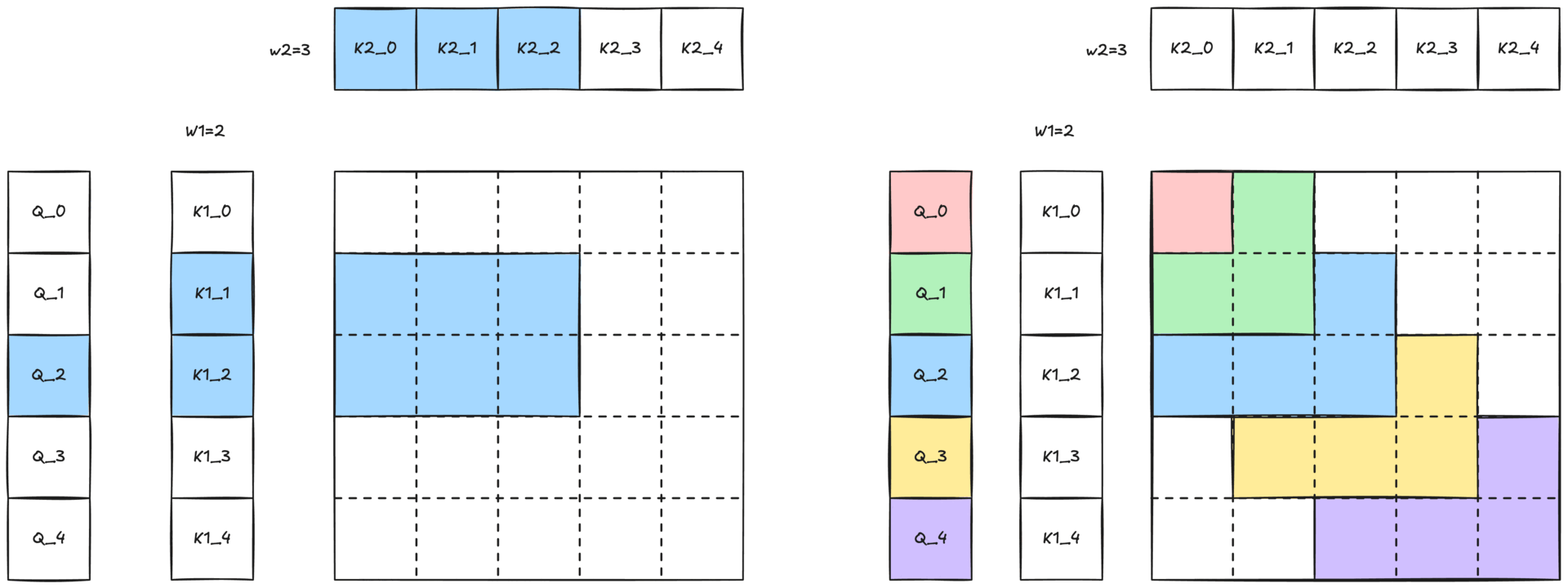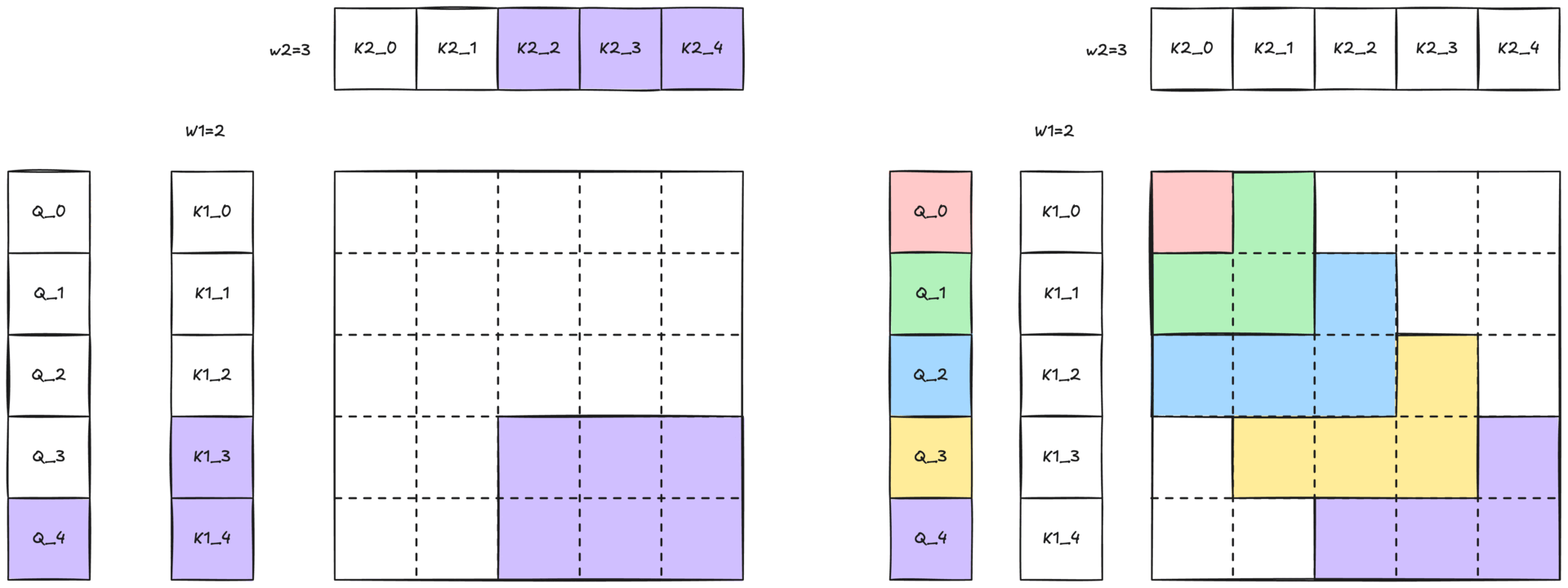
图 1:带有二维滑动窗口的 2-单纯注意力可视化。每个矩形表示一个查询 (Q) 和一对键 (K' 和 K) 之间的交互。蓝色矩形突出显示滑动窗口结构中特定的查询-键对交互。
二维滑动窗口注意力
图 2:滑动窗口注意力与 2-单纯滑动窗口注意力的比较
由于完整的 2-单纯注意力会随着序列长度呈三次增长 O(N³),因此处理整个序列是不切实际的。我们通过一个由两个窗口大小 W1 和 W2 定义的二维滑动窗口(如图 2-b 所示,并在图 1 中展示)来减轻这种成本。每个查询词元 Q[i] 只关注
- 沿第一维最近的 W1 个 K1[i] / V1[i] 对
- 沿第二维最近的 W2 个 K2[k] / V2[k] 对
这种局部性约束保持了 2-单纯注意力的表达能力,同时使计算变得可行。
图 3:带有二维滑动窗口的 2-单纯注意力示意图。与 Q 词元颜色相同的彩色区域表示查询可以关注键和值的二维邻域 (W1 × W2)。
TLX – Triton 低级扩展介绍
TLX (Triton Low-Level Extensions) 是 Triton DSL 的语言扩展,它结合了高性能和开发者生产力。它与 Triton 的高级 Python API 无缝集成,同时通过一组丰富的内部函数,为 GPU 内核执行添加了面向 warp 的、接近硬件的控制。TLX 原生支持 NVIDIA Hopper 和 Blackwell 架构,并具有可扩展的设计以支持未来的架构,包括潜在的 AMD GPU,它支持共享内存平铺、寄存器支持的累加器、warp 专用化、流水线执行和细粒度 warp 级同步。
快速 2-单纯注意力 – 硬件对齐设计
为了使内核真正高效并实现 SOTA 性能,我们在模型和内核之间进行了大量硬件对齐的协同设计。所提出的内核设计采用以下关键特性。
Tensor Core 友好
由于点积本质上是两个张量之间的二元运算 (dot_product),2-单纯注意力(详见附录 [3])中存在三个张量 (trilinear_product) 提出了一个根本性挑战:计算 无法 直接利用 Tensor Core。
为了解决这个限制,我们通过战略性预计算开发了一种 Tensor Core 兼容的方法。我们的解决方案将 三元 运算分解为 二元 组件:
- 首先,我们预计算 Q[i] 和 K1[s] 的元素乘积(公式 (c) 第 10 行),从而实现后续与 K2[t] 的乘法(公式 (c) 第 11 行)的 Tensor Core 计算。
- 类似地,我们预计算 V1[s] 和 V2[t] 的元素乘积(公式 (c) 第 13 行),允许高效地使用组合的 V12[s][t] 进行 P 的 Tensor Core 计算(公式 (c) 第 14 行)。
这种重新表述(如 公式 (c) 所示)将 2-单纯滑动窗口注意力转换为 Tensor Core 友好 的设计,并保持了数学等价性。

注意: ⊙ 表示元素级乘法
我们考虑了两种方法来实现 Tensor Core 友好的 GPU 内核公式
- 单独的内核:在一个内核中实现预计算,将结果 (Precomputed-QK1 和 Precomputed-V1V2) 写入全局内存 (GMEM),并使用自定义的点积注意力内核。
- 融合内核:将整个公式 (c) 集成到一个注意力内核中。
第一种方法存在一个显著的缺点:峰值内存使用量大幅增加。具体来说,Precomputed-QK1 需要比 Q 多 W1 倍的内存,而 Precomputed-V1V2 需要比 V 多 (W1 + W2) 倍的内存。对于典型值,例如 W1 = 32,W2 = 512,并且 N 随着模型的上下文窗口缩放,内存开销对于包含 2-单纯注意力的模型训练来说变得 prohibitive。因此,我们采用了第二种方法,实现了一个用于 2-单纯滑动窗口注意力的端到端融合内核。
非对称滑动窗口
非对称滑动窗口 (W1 ≠ W2) 与 对称滑动窗口 (W1 = W2):实验结果 [1] 表明,当 W1 x W2 保持不变(保持相同的 Tensor Core TFLOPs)时,非对称配置通常会产生更好的模型质量。为了硬件对齐,我们采用较小的 W1 和较大的 W2 值(在我们的实现中 W1 = 32,W2 = 512),原因如下:
- Tensor Core 友好:较大的 W2 值增加了 Tensor Core 与 CUDA Core 的比率,提高了 Tensor Core 计算效率。
- 在共享内存 (SMEM) 中保留所有 K1 和 V1 瓦片:根据算法 2,每个 K1/V1 瓦片形状为 [1, D],需要 W1 次加载。对于较小的 W1,我们可以在循环外将所有 W1 个 K1/V1 瓦片以 [W1, D] 的形状加载到 SMEM 中,然后在 W1 循环期间将单个 [1, D] 瓦片从 SMEM 重新加载到寄存器中。对于 W1 = 32,D = 128,以及 BFloat16 精度,K1 和 V1 瓦片的总大小为 16KB,约占 H100 SMEM 容量的 7%。
头部组平铺 – Pack GQA
在滑动窗口注意力中,每个查询 Q 词元选择不同的 K 词元集。当沿着序列维度进行平铺时,我们必须屏蔽掉某些 QK 对,导致计算浪费。这种低效率在 2D 滑动窗口注意力中被放大。例如,在 BLOCK_M = 64,BLOCK_KV = 128,N = 8192,W1 = 32 和 W2 = 512 的情况下,根据附录 [1] 中的计算。大约 73.2% 的计算被浪费。
受 Native Sparse Attention [5] 内核设计的启发,我们将同一 GQA KV 头组的所有查询头打包到一个瓦片中,而不是沿着序列维度进行平铺。这种方法消除了大部分二维滑动窗口掩码计算。在我们最终的实现中,滑动窗口掩码仅在最初几个 CTA 的最后一个 W2 循环迭代中需要,将浪费率从 73.2% 降低到 1.35%(详细计算见附录 [1])。
权衡考虑:头部维度平铺的缺点是查询头数量配置的灵活性降低。WGMMA [6] 指令要求最小 M = 64。低于 64 的配置也会浪费计算。为了平衡掩码效率和模型灵活性,我们可以将连续的 Q 词元与 Q 头打包到一个瓦片中,以满足 64 大小要求(类似于 FA3 解码内核中的 PACK_GQA)。虽然原始论文使用 GQA 比率 64,但我们的实现使用 128,以在不同的 Q 瓦片上实现两个消费者 warp-group 分区,用于峰值 TFLOPs 的基准测试。
V1 瓦片优化
考虑操作 C = A @ B。WGMMA 指令允许矩阵 A 存储在寄存器内存 (RMEM) 或 SMEM 中,而矩阵 B 必须驻留在 SMEM 中。输出瓦片 C 存储在 RMEM 中。对于注意力中的 PV12 GEMM,P(QK12 GEMM 的输出)驻留在 RMEM 中,V2(通过 TMA 加载)驻留在 SMEM 中。然而,V1 和 V2 公式 (c) 的广播乘法操作要求两个操作数都在 RMEM 中。这需要将 V2 从 SMEM 加载到 RMEM,执行元素级计算生成 V12,然后将 V12 存储回 SMEM。这是一个低效的过程。
我们观察到 PV GEMM 的输出驻留在 RMEM 中,并且由于 V1 沿着 PV12 的点积维度广播,因此在与 P 进行点积之前或之后应用 V1 到 V2 在数学上是等价的。
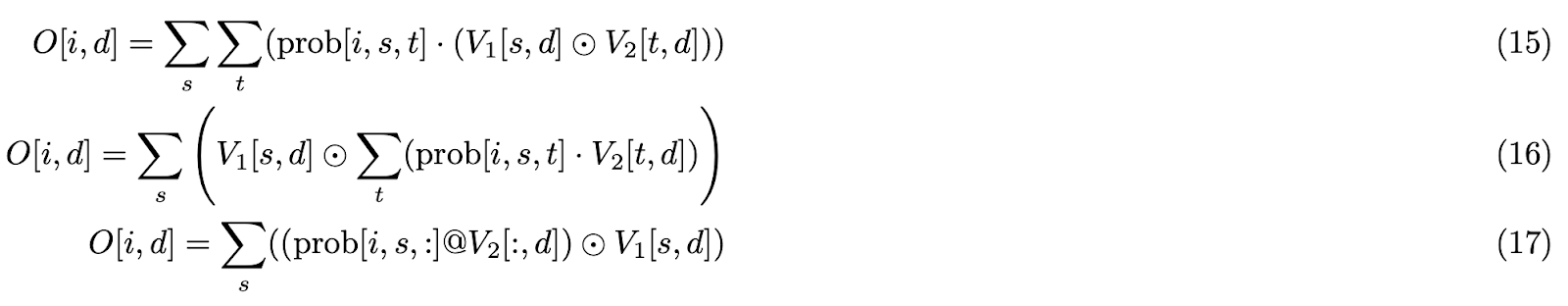
因此,我们优化了算法,将 V1 瓦片直接应用于 PV GEMM 输出,消除了冗余的 SMEM ↔ RMEM 加载/存储操作。
注意: 为什么计算 Q⊙K1 而不是 K1⊙K2?因为
- K1⊙K2 无法在 w1 循环中预计算。预计算所有组合需要将大小为 w1 × w2 × D 的数据存储在 SMEM 中,这太大了,无法容纳。
- K1⊙K2 的结果驻留在 RMEM 中,造成了与 V1⊙V2 相同的低效率。
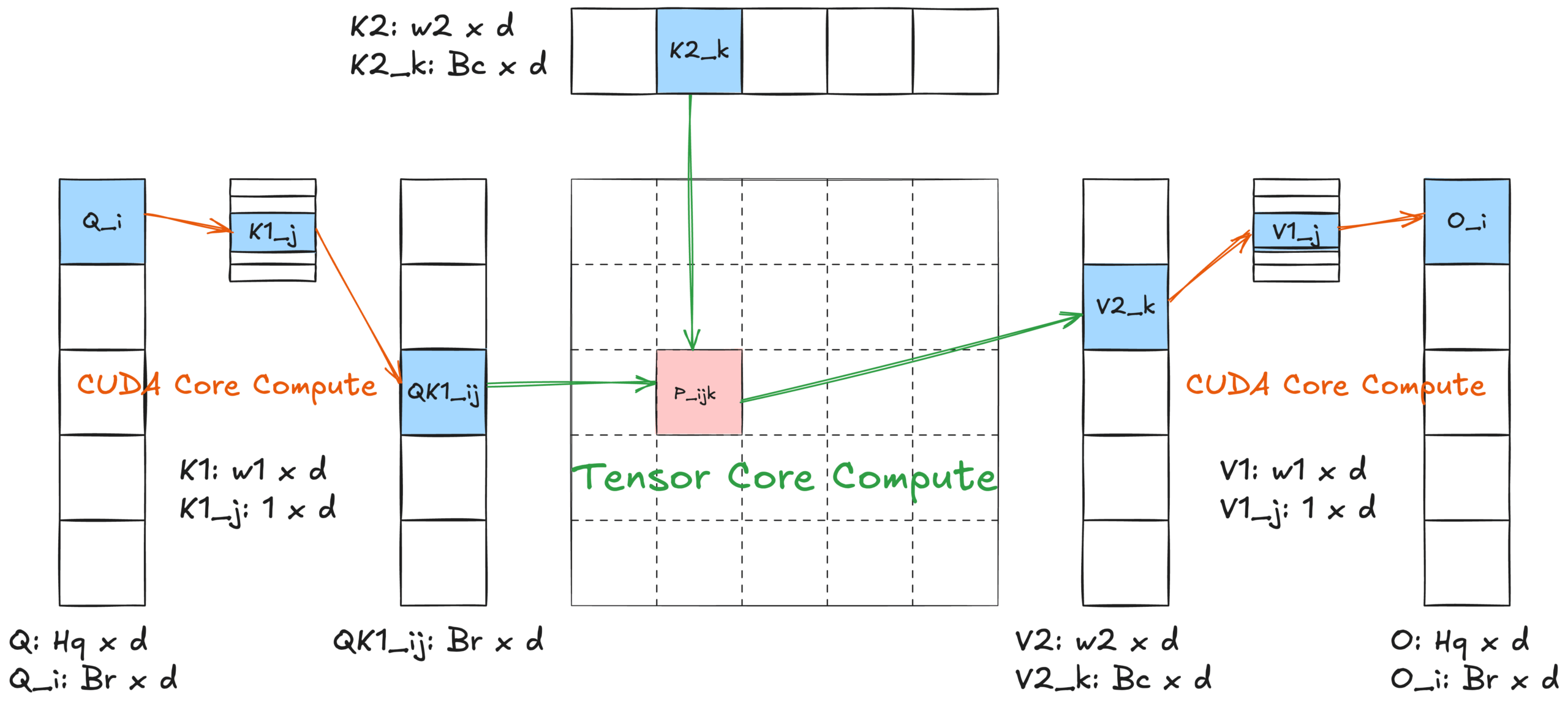
图 4:算法 2 内核设计示意图
基于所有这些特性和 FlashAttention2 [3] 算法,我们实施了融合的 2-单纯注意力内核算法——算法 2。与点积注意力相比,它引入了两个嵌套的 w1 和 w2 内循环,其中最内层循环与 FlashAttention2 的内循环非常相似。

算法 2 进行了更多的 CUDA Core 计算,引发了 CUDA Core 是否会成为 2-单纯注意力内核性能瓶颈的问题。我们的分析表明 CUDA Core 不是限制因素;详细论证在附录 [5] 中提供。
采用 TLX 的现代 GPU 技术
尽管实施了上述所有优化,我们的 Triton 内核实现仍远低于最先进的性能。我们最佳的前向注意力内核只能实现 34% 的 Tensor Core 利用率,而 FlashAttention3 [4] 拥有令人印象深刻的 75% 利用率。
对生成的 PTX 代码的分析显示,软件流水线和自动 warp 专用化未能与内核协同工作。软件流水线编译器后端无法执行必要的模式匹配并跳过了优化,而 warp 专用化则触发了 2-单纯注意力实现特有的编译错误。
为了在 Hopper 架构上快速集成 FlashAttention3 [4] 等现代注意力优化技术,包括 warp 专用化、跨 warpgroup 重叠(乒乓调度)和 warpgroup 内重叠(计算流水线),我们使用 TLX 重写了内核。我们开发了三个不同的版本:
- 内核 1:前向 + Warp 专用化(附录 [4] 算法 3 中描述)
- 内核 2:前向 + Warp 专用化 + 计算流水线
- 内核 3:前向 + Warp 专用化 + 乒乓调度
注意: 如果您想了解更多关于 Hopper 上的 Warp 专用化、计算流水线和乒乓调度,请参阅论文 FlashAttention3 [4] 和 Colfax 博客。
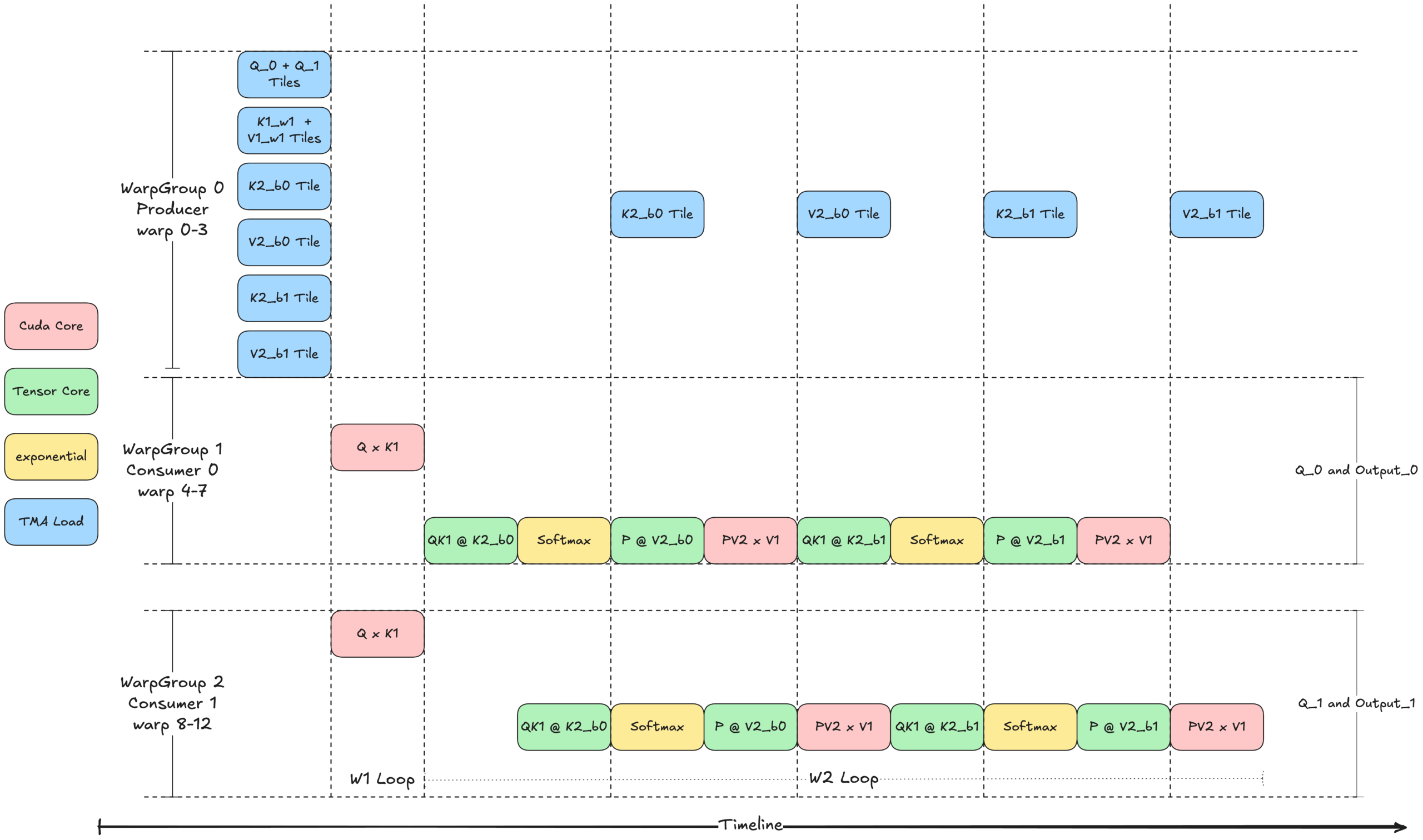
图 5 展示了内核 3 的思想:带有乒乓调度的 Warp 专用化,使用共享内存 (SMEM) 中的两个缓冲区和两个消费者组。生产者 (WarpGroup 0) 首先发出 TMA 加载指令,用于两个 Q 瓦片、一个 K1 瓦片、一个 V1 瓦片以及两个 K2 和 V2 瓦片。消费者 warp 组等待相应的瓦片到达后执行计算。生产者和消费者之间的同步通过屏障进行管理。
每个消费者组在不同的 Q 瓦片上操作,但共享相同的 K1、V1、K2 和 V2 瓦片,同时为不同的输出瓦片生成结果。为了最大限度地提高效率,乒乓调度确保在任何时候只有一个 warp 组执行 Tensor Core (WGMMA) 操作。
图 6 是内核 1 WS(顶部)和带有乒乓调度的内核 3 WS(底部)的执行轨迹比较图,使用 Proton [8] 捕获。这些轨迹突出显示了乒乓调度如何减少内部 w2 循环中的 Tensor Core 气泡,从而提高 Tensor Core 资源的利用率。
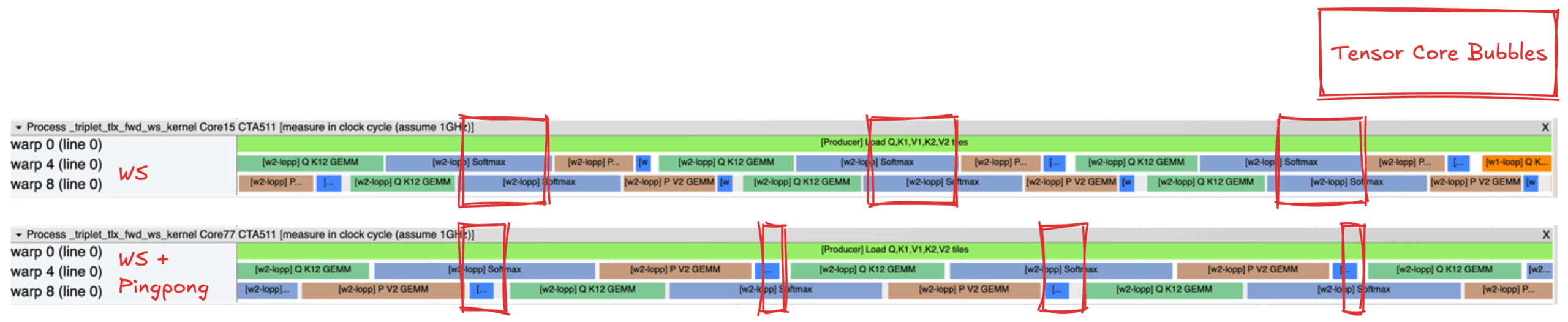
图 6:内核 1 WS(顶部)和内核 3 WS + 乒乓(底部)的 Tensor Core 气泡示意图
基准测试结果显示,从内核 1 到内核 3,性能提升约为中性到 1%。微小的增益可能反映了内核 1 已经实现了 GEMM 和 Softmax 操作之间的部分重叠。目前,内核 1 实现了 60% 的 Tensor Core 利用率,这比之前纯 Triton 实现的 34% Tensor Core 利用率有了显著提升。内核 2 由于寄存器溢出问题导致性能下降。理论上,Warp 专用化、计算流水线和乒乓调度的结合应该会产生最佳性能。
基准测试
根据附录 [5] 中的分析,Tensor Core TFLOPs 显著超过 CUDA Core TFLOPs。因此,为简化起见,我们仅将 Tensor Core TFLOPs 作为内核性能的主要指标。
请注意 2D 滑动窗口注意力的以下行为,这里我们假设 W1 ≤ W2:
- 当总序列长度 N < W1 时:该机制在 W1 和 W2 上均作为 2D 因果注意力运行。
- 当 W1 ≤ N < W2 时:该机制在 W1 上作为 1D 滑动窗口运行,在 W2 上作为 1D 因果注意力运行。
- 当 N ≥ W2 时:该机制作为完整的 2D 滑动窗口运行。
有关 Tensor Core TFLOPs 计算的详细信息,请参阅附录 [2]。
基准测试设置详见 [9]。我们在图 5 中展示了峰值 588 TFLOPs 的结果。
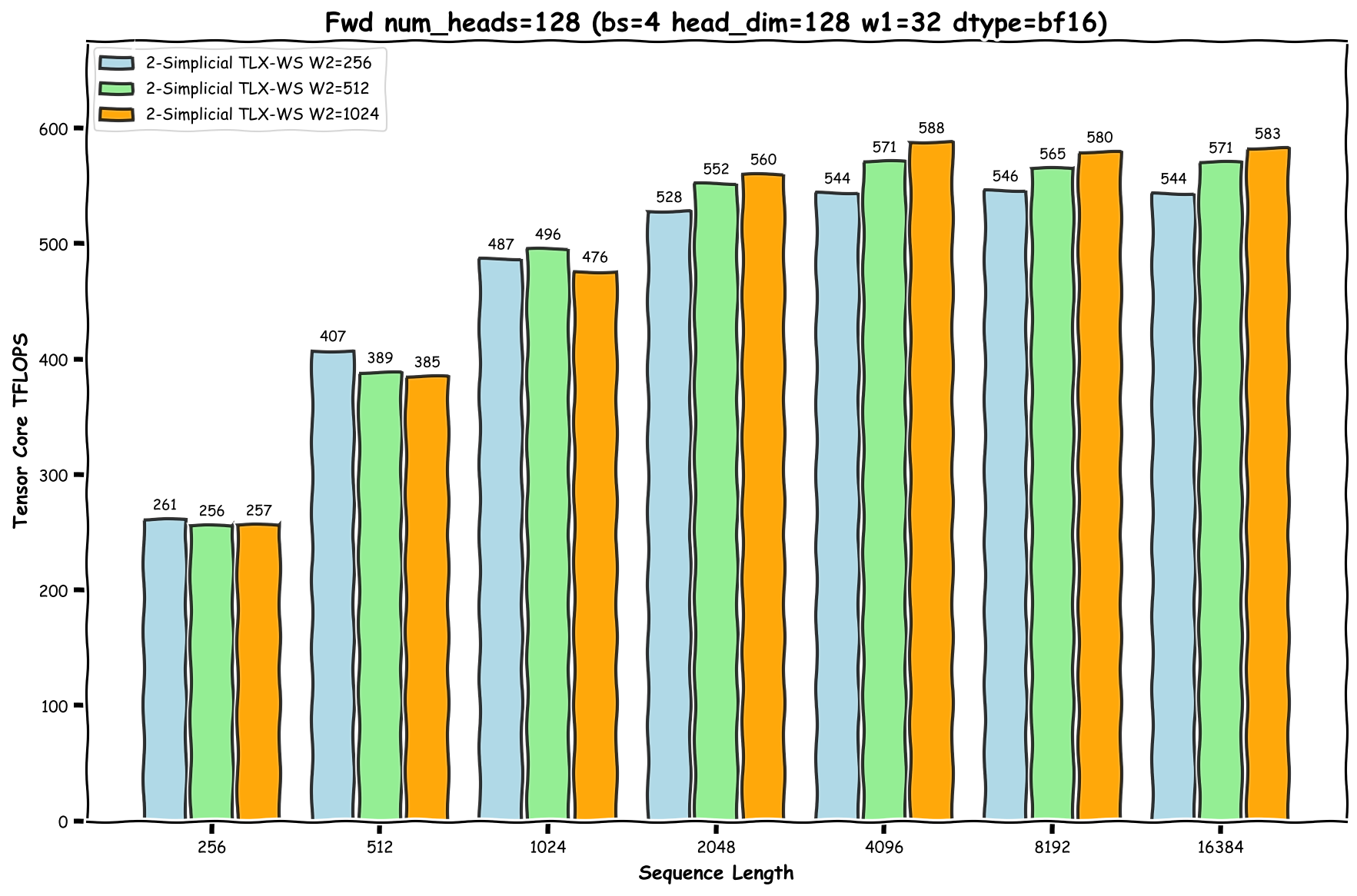
图 7:快速 2-单纯注意力内核 - 前向传播的基准测试结果
注意:短序列长度会导致性能不佳,因为存在掩码瓦片。具体来说,对于 i < W2 的词元,必须对最终瓦片应用因果掩码以确保 j ≤ i。这会降低这些词元最终瓦片的计算密度,并增加掩码计算带来的 cuda core 开销。相反,对于 i ≥ W2 且 W2 % BLOCK_KV = 0 的词元,我们可以从 i-W2+1 循环到 i,而无需掩码,因为所有瓦片都是完整的。由于短序列长度中 i < W2 的词元比例更高,因此整体性能会受到影响。
我们使用 FlashAttention3 (FA3) 作为点积注意力的参考实现。为了确保每个查询词元具有相同的计算工作负载,具体来说,在点积注意力和 2-单纯注意力中与相同数量的不同 KV 词元进行交互,我们将 FA3 的 KV 序列长度设置为 W1 x W2,不带因果掩码。我们的基准测试结果显示,FA3 实现了高达 750 TFLOPs,这表明我们最好的 2-单纯注意力实现达到了 FA3 峰值性能的约 78.4%。
我们还测量了 TLX 版本 FlashAttention [10] 的峰值 TFLOPs,结果如下:
| FA TLX-WS 内核 | FA TLX-WS + 计算流水线内核 | FA TLX-WS + 计算流水线 + 乒乓内核 | |
| 峰值 TFLOPs | 590 | 680 | 717 |
我们的快速 2-单纯 TLX-WS(内核 1)内核实现了与 FA TLX-WS 几乎相同的峰值 TFLOPs。剩余的性能差距主要源于计算流水线和乒乓优化尚未在 2-单纯注意力内核中完全发挥作用,这是我们计划在未来工作中解决的领域。
结论
在这篇博客中,我们提出了一种设计硬件对齐的 2-单纯注意力内核算法的综合方法,展示了系统优化如何实现强大性能。我们介绍了一种实现融合 2-单纯注意力内核的简洁算法,并采用了 Hopper 的一些特性,例如用于标准点积注意力的 FlashAttention 2.X。
未来仍有几个领域有待开发:启用计算流水线、开发用于反向传播和解码形状的快速内核、实现持久调度以及沿 N 维度划分消费者组以支持小 GQA 比率。
我们希望这项工作能为寻求通过硬件对齐设计改进注意力机制的研究人员提供宝贵的见解!
致谢
我们衷心感谢 Vijay Krishnamoorthy、Jing Zhang、Yang Chen、Mark Saroufim 和 Bert Maher 对这篇博客文章的审阅和宝贵反馈。我们还要感谢 Daohang Shi、Peng Chen 和 Manman Ren 在解决 TLX 相关问题上的帮助。
参考文献
[1] 快速而简洁:Triton 中的 2-单纯注意力:https://arxiv.org/pdf/2507.02754
[2] TLX – Triton 低级扩展:https://github.com/facebookexperimental/triton/tree/tlx
[3] 逻辑与 2-单纯 Transformer:https://arxiv.org/abs/1909.00668
[3] FlashAttention-2:https://arxiv.org/abs/2307.08691
[4] FlashAttention-3:https://arxiv.org/abs/2407.08608
[5] 原生稀疏注意力:https://arxiv.org/abs/2502.11089
[6] PTX WGMMA 矩阵形状:https://docs.nvda.net.cn/cuda/parallel-thread-execution/#asynchronous-warpgroup-level-matrix-shape
[7] H100 SXM:https://resources.nvidia.com/en-us-gpu-resources/h100-datasheet-24306
- BF16 Tensor Core:989 TFlops
- BF16 Cuda Core:134 TFlops
- BF16 Tensor Core 与 Cuda Core 之比 = 7.38x
[8] Proton – Triton 分析器:https://github.com/triton-lang/triton/tree/main/third_party/proton
[9] 基准测试设置
- H100 SXM 功率设置:700W
- FlashAttention v2.8.3
- CUDA 12.6
附录
[1] 2D SWA 浪费计算的计算
------------------------------ Parameters: M=64, KV=128, N=8192, W1=32, W2=512, D=128 Tiling Sequence: Efficiency: 26.80% Waste: 73.20% Tiling Heads: Efficiency: 98.65% Waste: 1.35%
[2] 2-单纯注意力前向传播的 Tensor Core TFLOPs 计算
[3] 点积和三线性积
def dot_product(A, B): """ Standard dot product (matrix multiplication) Input: A in [M, K], B in [N, K] Output: C in [M, N] This is equivalent to A @ B.T """ M, K = A.shape N, K2 = B.shape assert K == K2, "Inner dimensions must match" C = np.zeros((M, N)) for i in range(M): for j in range(N): C[i][j] = sum(A[i][inner_k] * B[j][inner_k] for inner_k in range(K)) return C def trilinear_product_2D_to_3D(A, B1, B2): """ Trilinear product for computing 3D attention logits Input: A in [M, K], B1 in [N, K], B2 in [N, K] Output: C in [M, N, N] Each element C[i,j,k] is the sum of element-wise products of A[i,:], B1[j,:], and B2[k,:] along the K dimension """ M, K = A.shape N, K1 = B1.shape N2, K2 = B2.shape assert K == K1 == K2, "All K dimensions must match" assert N == N2, "N dimensions must match" C = np.zeros((M, N, N)) for i in range(M): for j in range(N): for k in range(N): C[i][j][k] = sum(A[i][inner_k] * B1[j][inner_k] * B2[k][inner_k] for inner_k in range(K)) return C def trilinear_product_3D_to_2D(A, B1, B2): """ Trilinear product for aggregating with 3D attention weights Input: A in [M, N, N], B1 in [N, K], B2 in [N, K] Output: C in [M, K] Uses 3D attention weights A to aggregate information from B1 and B2 """ M, N, N2 = A.shape assert N == N2, "A must be square in last two dimensions" N3, K = B1.shape N4, K2 = B2.shape assert N == N3 == N4, "N dimensions must match" assert K == K2, "K dimensions must match" C = np.zeros((M, K)) for i in range(M): for k in range(K): C[i][k] = sum(A[i][a][b] * B1[a][k] * B2[b][k] for a in range(N) for b in range(N)) return C
[4] 算法 3:前向 + Warp 专用化

[5] CUDA Core 计算的理论分析
为简化分析,我们省略了批量维度 (B) 并采用以下符号:
- Hq:查询头数
- N:序列长度
- D:头部维度
- Hkv:键值头数 (= 1),在此计算中也省略
- BLOCK_M:查询头部的瓦片大小 (= Hq)
- BLOCK_KV:KV 序列长度维度的瓦片大小
Tensor Core TFLOPs
N × Hq × D × W1 × W2 × 2 × 2 = 4 × N × Hq × D × W1 × W2
CUDA Core TFLOPs(仅计算 2-单纯注意力引入的 CUDA Core TFLOPs)
QK1 计算
- 每个 CTA:W1 × BLOCK_M × D
- CTA 数量:N
- 总计:N × W1 × BLOCK_M × D
PV2V1 计算
- 每个 CTA:W1 × (W2 / BLOCK_KV) × BLOCK_M × D
- CTA 数量:N
- 总计:N × W1 × (W2 / BLOCK_KV) × BLOCK_M × D
组合 CUDA Core TFLOPs
N × W1 × BLOCK_M × D + N × W1 × (W2 / BLOCK_KV) × BLOCK_M × D = N × W1 × BLOCK_M × D × (1 + W2 / BLOCK_KV)
比率分析
Tensor Core / CUDA Core = 4 × W2 × BLOCK_KV / (BLOCK_KV + W2)
例如,在 BLOCK_KV = 128 和 W2 = 512 的情况下,Tensor Core TFLOPs 大约超过 CUDA Core TFLOPs 410 倍,其中 Tensor Core 比 Cuda Core 快约 7.38 倍 [7]。因此,CUDA Core 计算 不会 成为 2-单纯注意力内核的瓶颈。