在 Opacus – PyTorch 中实现快速梯度裁剪和幻影裁剪

介绍和背景

差分隐私随机梯度下降 (DP-SGD) 是使用差分隐私训练机器学习模型的经典方法。与非隐私对应的随机梯度下降相比，它涉及以下两项修改。

逐样本梯度裁剪：对小批量中的每个样本进行梯度裁剪，确保其范数在每次迭代中至多为一个预设值，“裁剪范数” C。
添加噪声：在每次迭代中，根据裁剪范数和隐私参数，向平均裁剪梯度添加预设方差的高斯噪声。

第一个变化，逐样本梯度裁剪，引入了额外的复杂性，因为它通常需要实例化逐样本梯度。

Opacus 是 DP-SGD 的 PyTorch 实现。Opacus 通过采用钩子函数来解决上述任务，这些函数允许干预特定事件，例如前向和后向传播。有关 Opacus 的更多详细信息，我们鼓励读者回顾之前的博客文章：DP-SGD 算法解释、Opacus 中高效的逐样本梯度计算和Opacus 中更多层的逐样本梯度高效计算。

虽然 Opacus 与朴素方法相比提供了显著的效率提升，但实例化逐样本梯度的内存成本很高。特别是，内存使用量与批量大小乘以可训练参数的数量成比例。因此，内存限制了 Opacus 使用小批量大小和/或小型模型，这显著限制了其应用范围。

我们将快速梯度裁剪和幻影裁剪引入 Opacus，使开发人员和研究人员能够无需实例化逐样本梯度即可执行梯度裁剪。例如，这允许在单个 16GB GPU 上，以 1024 的批量大小微调 BERT 的 7M 参数，其内存与使用 PyTorch（不应用 DP-SGD）相当。相比之下，Opacus 的先前版本在相同设置下支持的最大批量大小约为 256。我们提供了一个教程，说明如何在 Opacus 中使用快速梯度裁剪，并以上述任务为例。

快速梯度裁剪和幻影裁剪

这些技术的核心思想基于以下观察：假设已知逐样本梯度范数，则可以通过在重新加权的损失函数 $ \bar{L} $ 上进行反向传播来实现梯度裁剪。此损失函数定义为 $ \bar{L} = \sum_{i} R_{i} L_{i} $，其中 $ R_i = \min\left(\frac{C}{C_i}, 1\right) $ 是根据逐样本梯度范数 $ {C_i} $ 计算的裁剪系数，$ {L_i} $ 是逐样本损失。

上述想法乍一看可能有些循环，因为它似乎需要实例化逐样本梯度才能计算逐样本梯度范数。然而，对于神经网络架构中某些广泛使用的组件，例如全连接/线性层，确实可以在单个反向传播过程中获得逐样本梯度范数，而无需逐样本梯度。这提出了一种包含两次反向传播的工作流程：第一次计算逐样本梯度范数，第二次计算聚合（非逐样本）裁剪梯度。第二次反向传播只是标准的批处理反向传播。

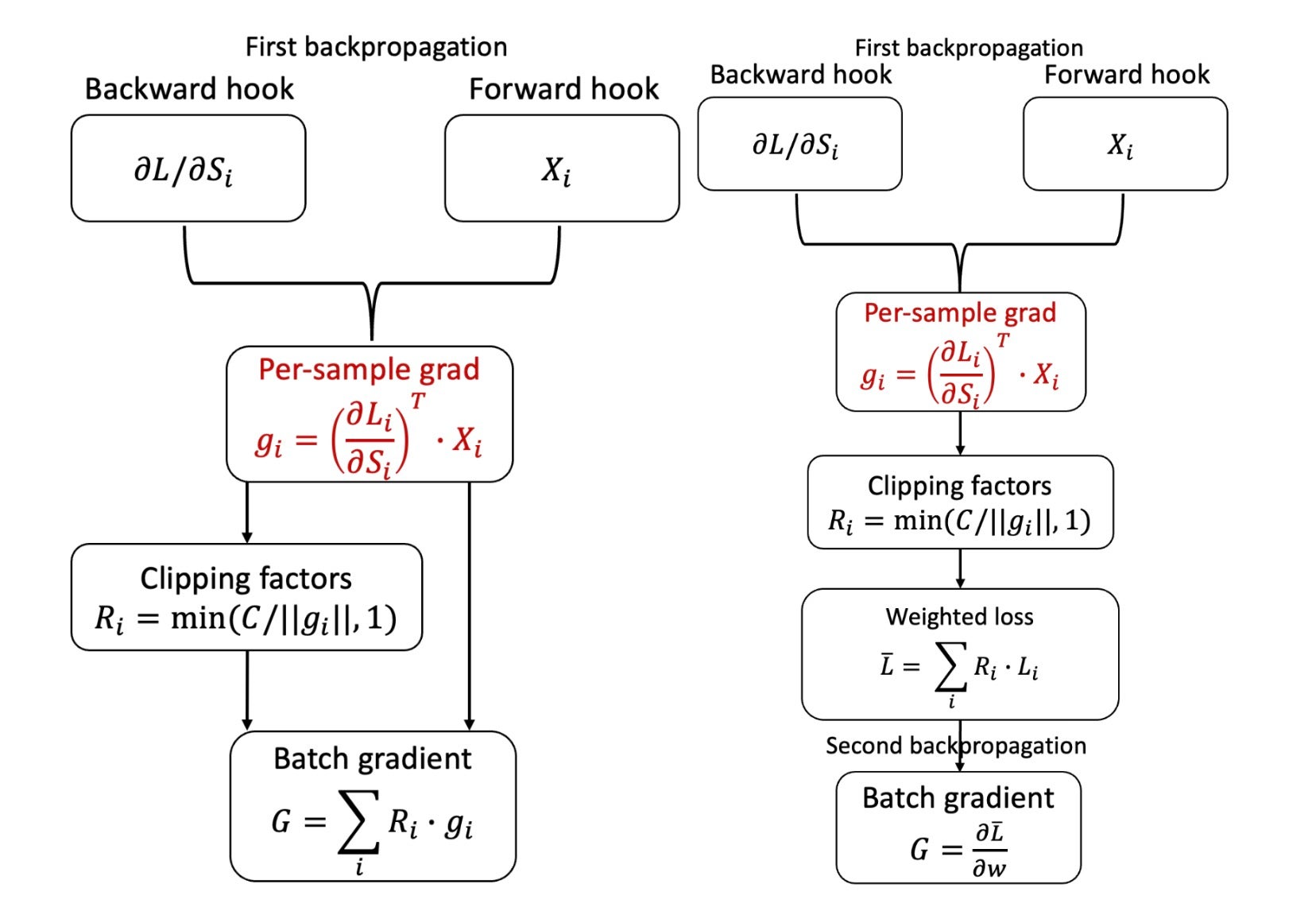
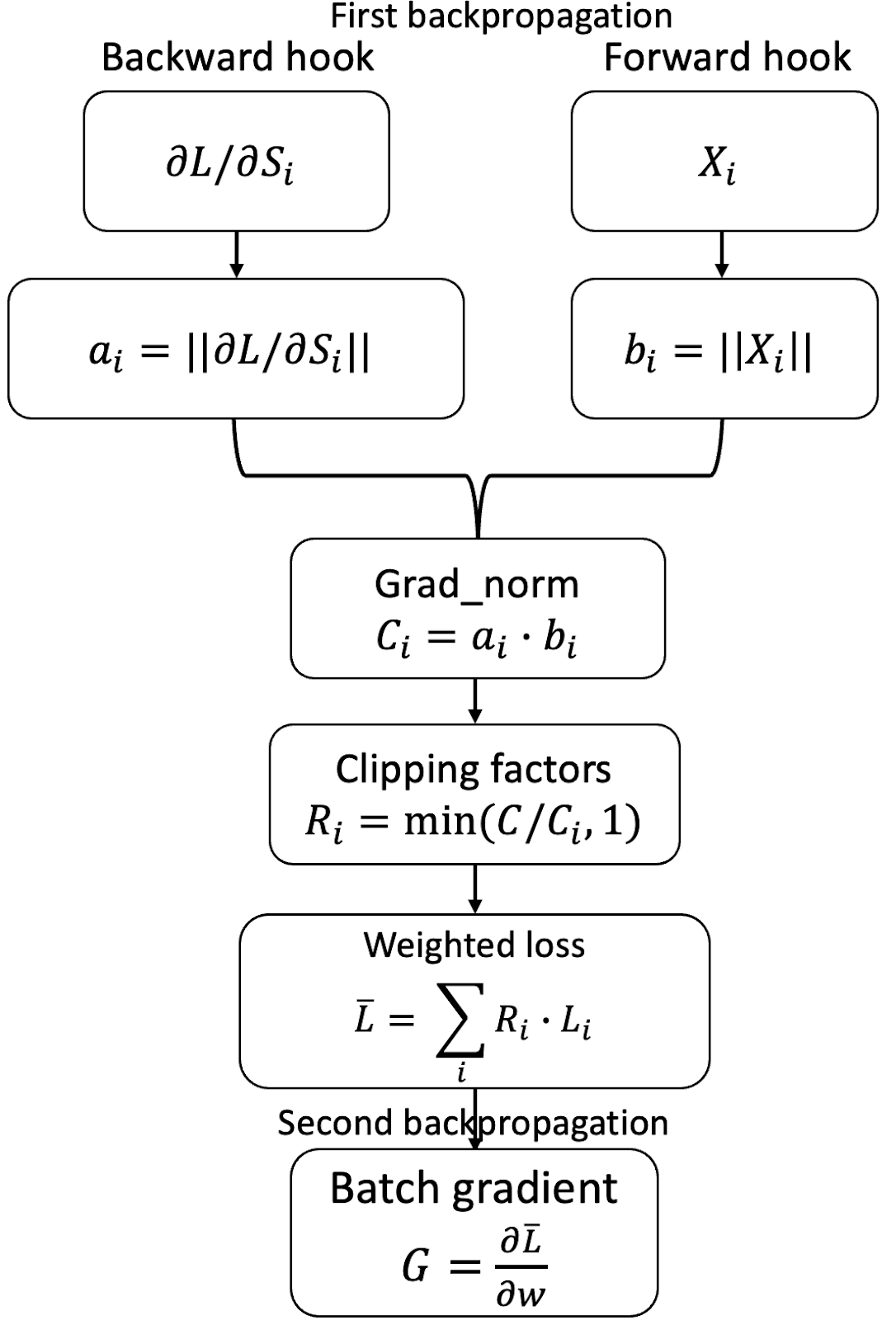
图 1：香草版 Opacus（左上）、快速梯度裁剪（右上）和 幻影裁剪（底部）之间的比较。我们用红色标记了成为内存瓶颈的梯度实例化。对于香草版 Opacus，它必须实例化逐样本梯度。快速梯度裁剪为每个层实例化逐样本梯度以计算其范数，一旦反向传播进入下一层，该梯度将立即释放。幻影裁剪直接从逐样本激活梯度和逐样本激活工作，并避免了梯度实例化的需要。

快速梯度裁剪
在快速梯度裁剪中，逐样本梯度范数分三步计算

对于每个层，实例化逐样本梯度并计算其范数。
然后立即丢弃逐样本梯度。
将每个层的（平方）逐样本梯度范数求和以获得总体（平方）逐样本梯度范数。

幻影裁剪
幻影裁剪扩展了快速梯度裁剪的方法，它利用了事实，即对于线性层¹，逐样本梯度范数可以仅根据激活梯度和激活来计算。具体来说，令 backprops 和 activations 分别为逐样本激活梯度和激活，维度分别为 batch_size ✕ output_width 和 batch_size ✕ input_width。逐样本梯度是两者的外积，需要 O(batch_size ✕ input_width ✕ output_width) 的时间和空间。

幻影裁剪技巧不是计算逐样本梯度，而是计算 backprops 和 activations 的（平方）范数，并逐样本地取它们的乘积，从而得到梯度的（平方）范数。这需要 O(batch-size ✕ (input_width + output_width)) 的时间，并且需要 O(batch-size) 的空间来存储。由于逐样本激活和逐样本激活梯度已经存储，因此只需要额外的内存来存储范数。

快速梯度裁剪与幻影裁剪的关系

快速梯度裁剪和幻影裁剪是互补的技术。快速梯度裁剪可以应用于任何类型的层，而幻影裁剪对于受支持的层来说是严格更好的技术。
当层不受幻影裁剪支持时，我们的实现会自动切换到快速梯度裁剪。

如何在 Opacus 中使用快速梯度裁剪

训练循环与标准 PyTorch 循环相同。与以前的 Opacus 一样，我们使用 PrivacyEngine()，它“净化”模型和优化器。为了启用幻影裁剪，使用了参数 grad_sample_mode="ghost"。此外，make_private() 将损失准则作为额外输入并对其进行净化。这允许我们在 loss.backward() 中隐藏两次反向传播和中间的损失重新缩放。

from opacus import PrivacyEngine
criterion = nn.CrossEntropyLoss() # example loss function

privacy_engine = PrivacyEngine()
model_gc, optimizer_gc, criterion_gc, train_loader, = privacy_engine.make_private(
        module=model,
        optimizer=optimizer,
        data_loader=train_loader,
        noise_multiplier=noise_multiplier
        max_grad_norm=max_grad_norm,
	 criterion=criterion,
        grad_sample_mode="ghost",
)

# The training loop below is identical to that of PyTorch

for input_data, target_data in train_loader:
    output_gc = model_gc(input_data) # Forward pass
    optimizer_gc.zero_grad()
    loss = criterion_gc(output_gc, target_data)
    loss.backward()
    optimizer_gc.step()  # Add noise and update the model

在内部，在第一次传播之前，我们启用钩子，这使我们能够捕获与前向和后向调用对应的逐层值。它们用于计算逐样本梯度范数。然后我们计算裁剪系数，重新缩放损失函数并禁用钩子，这使我们能够使用标准的 PyTorch 反向传播。

内存复杂度分析

考虑一个具有以下属性的多层神经网络

L：层数
d：最大层宽度
B：批量大小
K：不受支持/非线性层的数量

与普通 (PyTorch) SGD 相比，使用幻影裁剪的 DP-SGD 的内存开销是附加的 O(BL)，用于存储所有层的逐样本梯度范数。此外，如果存在不受支持的层 (如果 K≥1)，则需要额外的 O(Bd²) 内存来实例化该层的梯度。

内存基准测试

我们提供了各种设置下的内存使用结果。

微调 BERT

我们考虑私有微调 BERT 的最后三层用于文本分类任务的问题。基本模型有超过 1 亿个参数，我们微调最后三层：BertEncoder、BertPooler 和 Classifier，包含大约 7.6M 个参数。实验在具有 16 GB 内存的 P100 GPU 上运行。

下表报告了各种方法的最大内存和每次迭代所需的时间

	批次大小
	B = 32		B = 128		B = 512		B = 1024		B = 2048
	内存	时间	内存	时间	内存	时间	内存	时间
PyTorch SGD	236 MB	0.15 秒	1.04 GB	0.55 秒	5.27 GB	2.1 秒	12.7 GB	4.2 秒	OOM
DP-SGD	1,142 MB	0.21 秒	4.55 GB	0.68 秒	OOM		OOM		OOM
FGC DP-SGD	908 MB	0.21 秒	3.6 GB	0.75 秒	OOM		OOM		OOM
GC DP-SGD	362 MB	0.21 秒	1.32 GB	0.67 秒	5.27 GB	2.5 秒	12.7 GB	5 秒	OOM

在峰值内存占用方面，DP-SGD > FGC DP-SGD ≫ GC DP-SGD ≈ PyTorch SGD。此外，运行时间相似，因为大多数参数是冻结的，前向传播占用了大部分时间。

合成设置：内存分析

我们考虑以下设置来分析 PyTorch SGD、Vanilla DP-SGD 和幻影裁剪 (GC DP-SGD) 所使用的内存。

2 层全连接神经网络
- 输入：5120
- 隐藏层：2560
- 输出：1280
- 模型参数总数 = 15.6M
- 模型大小 = 62.5 MB
批量大小，不同值，如下表所示。

下表总结了每种方法在训练循环各个阶段的最大内存增加量（以 MB 为单位）。

批量大小	方法	模型到 GPU	前向传播	第一次反向传播	第二次反向传播	优化器步骤
32	PyTorch SGD	62.5	0.5	62.5	不适用	0
	Vanilla DP-SGD	62.5	0.47	3,663	不适用	162.5
	GC DP-SGD	62.5	0.47	63.13	50	125
2¹⁷	PyTorch SGD	62.5	1920	1932.5	不适用	0
	Vanilla DP-SGD	OOM
	GC DP-SGD	62.5	1920	2625	1932.5	125

行业用例

我们对一个内部的 Meta 用例测试了幻影裁剪 DP-SGD，该模型大小约为 100B，具有 40M 可训练参数。我们的初步结果表明，幻影裁剪 SGD 减少了 Vanilla DP-SGD 95% 的内存，并实现了与 PyTorch SGD 相当的内存使用。

结论

在这篇文章中，我们描述了 Opacus 中快速梯度裁剪和幻影裁剪的实现，它们能够以内存高效的方式训练具有差分隐私的机器学习模型。目前，幻影裁剪的实现仅适用于线性层，但正如系列第三部分所述，它可以扩展到“广义”线性层，例如卷积和多头注意力。当前的技术需要两个显式的反向传播步骤，这会增加运行时间。我们将探索在幻影裁剪基础上进行开发，例如用于缓解的簿记算法。

要了解有关 Opacus 的更多信息，请访问opacus.ai 和github.com/pytorch/opacus。

致谢

我们感谢 Iden Kalemaj、Darren Liu、Karthik Prasad、Hao Shi、Igor Shilov、Davide Testuggine、Eli Uriegas、Haicheng Wang 和 Richard Zou 提供的宝贵反馈和建议。

有方法可以将幻影裁剪扩展到非线性层。↩

在 Opacus 中启用快速梯度裁剪和幽灵裁剪