跳转到主要内容
博客

使用半结构化 (2:4) 稀疏性加速神经网络训练

作者： 2024 年 6 月 20 日2024 年 11 月 13 日暂无评论

在过去的一年里，我们已将半结构化 (2:4) 稀疏性支持添加到 PyTorch 中。只需几行代码，我们就能在 Segment-Anything 上将密集矩阵乘法替换为稀疏矩阵乘法，从而实现 10% 的端到端推理速度提升。

然而，矩阵乘法并非神经网络推理独有，它们在训练期间也会发生。通过扩展我们早期用于加速推理的核心原语，我们还能够加速模型训练。我们编写了一个替换的 nn.Linear 层 SemiSparseLinear，它能够在 NVIDIA A100 上实现 ViT-L 的 MLP 块中线性层的前向 + 反向传递 1.3 倍的 加速。

端到端来看，DINOv2 ViT-L 训练的实际运行时间减少了 6%，且开箱即用的准确度几乎没有下降（ImageNet top-1 准确度为 82.8 vs 82.7）。

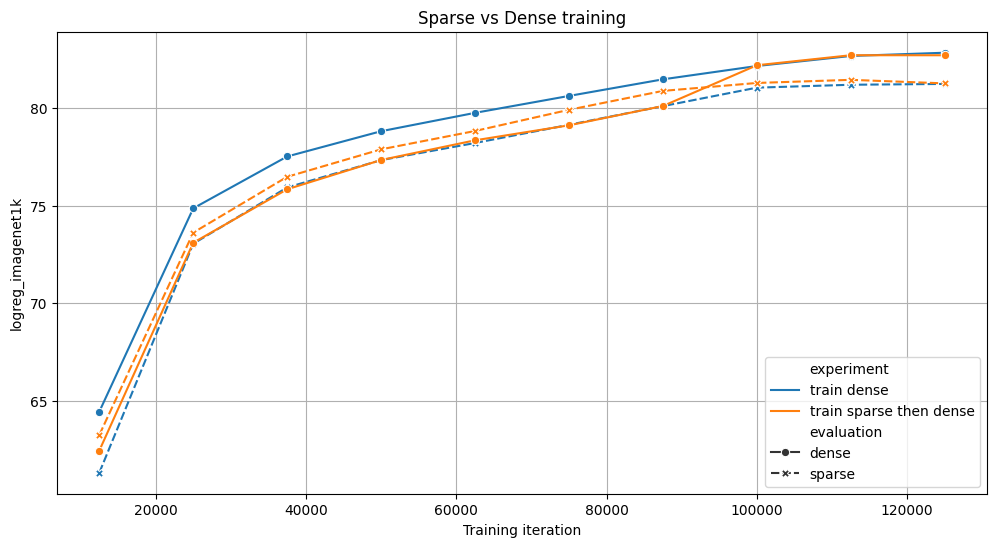
2 strategies for training a ViT model

我们比较了在 4 个 NVIDIA A100 上训练 ViT 模型 125k 次迭代的两种策略：完全密集（蓝色）或 70% 的训练是稀疏的，然后是密集（橙色）。两者在基准测试中都取得了相似的结果，但稀疏变体训练速度快了 6%。对于这两个实验，我们评估了有和没有稀疏性的中间检查点。

据我们所知，**这是第一个加速稀疏训练的开源实现**，我们很高兴能在 torchao 中提供用户 API。你只需几行代码即可尝试加速你自己的训练运行。

# Requires torchao and pytorch nightlies and CUDA compute capability 8.0+
import torch
from torchao.sparsity.training import (
    SemiSparseLinear,
    swap_linear_with_semi_sparse_linear,
)

model = torch.nn.Sequential(torch.nn.Linear(1024, 4096)).cuda().half()

# Specify the fully-qualified-name of the nn.Linear modules you want to swap
sparse_config = {
    "seq.0": SemiSparseLinear
}

# Swap nn.Linear with SemiSparseLinear, you can run your normal training loop after this step
swap_linear_with_semi_sparse_linear(model, sparse_config)

它是如何工作的？

稀疏性背后的总体思想很简单：跳过涉及零值张量元素的计算，以加速矩阵乘法。然而，仅仅将权重设置为零是不够的，因为密集张量仍然包含这些修剪过的元素，并且密集矩阵乘法核将继续处理它们，从而产生相同的延迟和内存开销。为了实现实际的性能增益，我们需要用智能地绕过涉及修剪过的元素的计算的稀疏核来替换密集核。

这些内核作用于稀疏矩阵，这些矩阵删除修剪过的元素并以压缩格式存储指定的元素。有许多不同的稀疏格式，但我们特别感兴趣的是**半结构化稀疏性**，也称为**2:4 结构化稀疏性**或**细粒度结构化稀疏性**，更一般地称为**N:M 结构化稀疏性**。

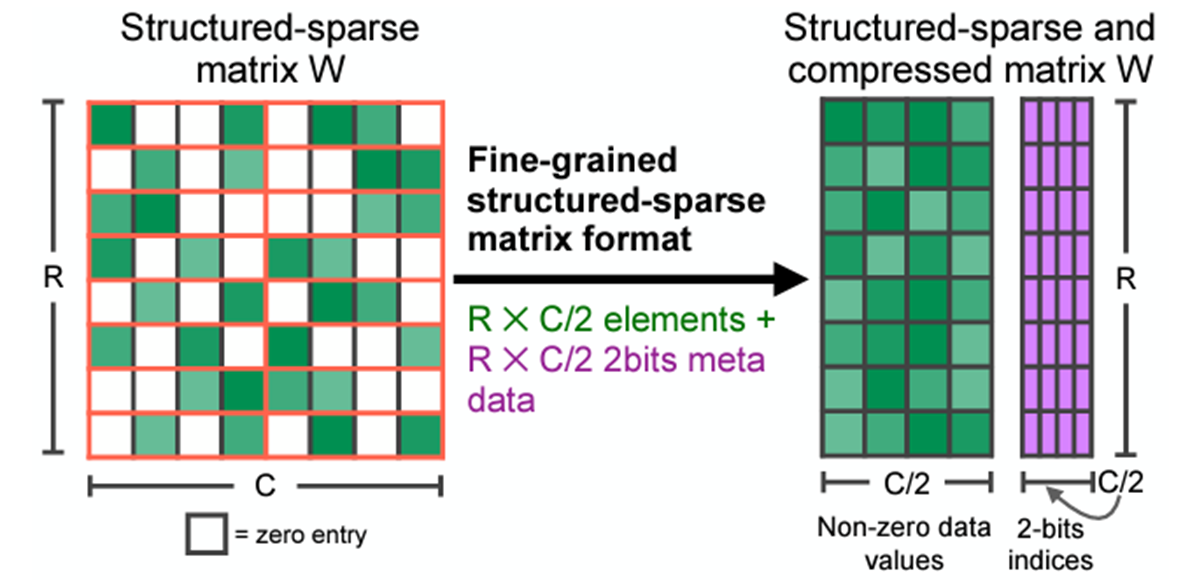
2:4 sparse compressed representation

2:4 稀疏压缩表示。原始 来源

2:4 稀疏矩阵是一个矩阵，其中每 4 个元素中最多有 2 个非零元素，如上图所示。半结构化稀疏性之所以具有吸引力，是因为它在性能和准确性之间找到了一个完美的平衡点。

  1. 自 Ampere 架构以来的 NVIDIA GPU 为这种格式提供硬件加速和库支持 (cuSPARSELt)，矩阵乘法速度最高可达 1.6 倍。
  2. 修剪模型以适应这种稀疏模式，其准确性下降不如其他模式那样严重。NVIDIA 的 白皮书 显示，修剪然后重新训练能够恢复大多数视觉模型的准确性。
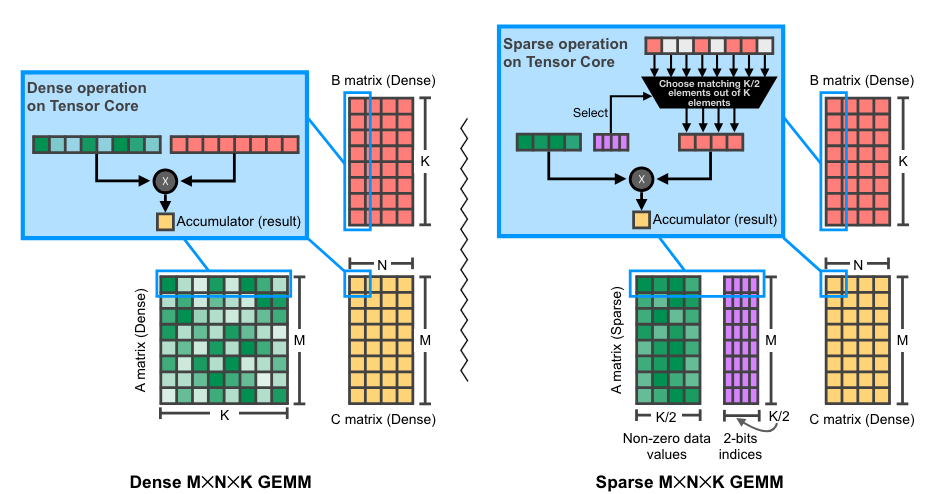
Illustration of 2:4 (sparse) matrix multiplication on NVIDIA GPUs

NVIDIA GPU 上 2:4 (稀疏) 矩阵乘法的图示。原始 来源

使用半结构化稀疏性加速推理很简单。由于我们的权重在推理过程中是固定的，我们可以提前（离线）修剪和压缩权重，并存储压缩的稀疏表示而不是密集张量。

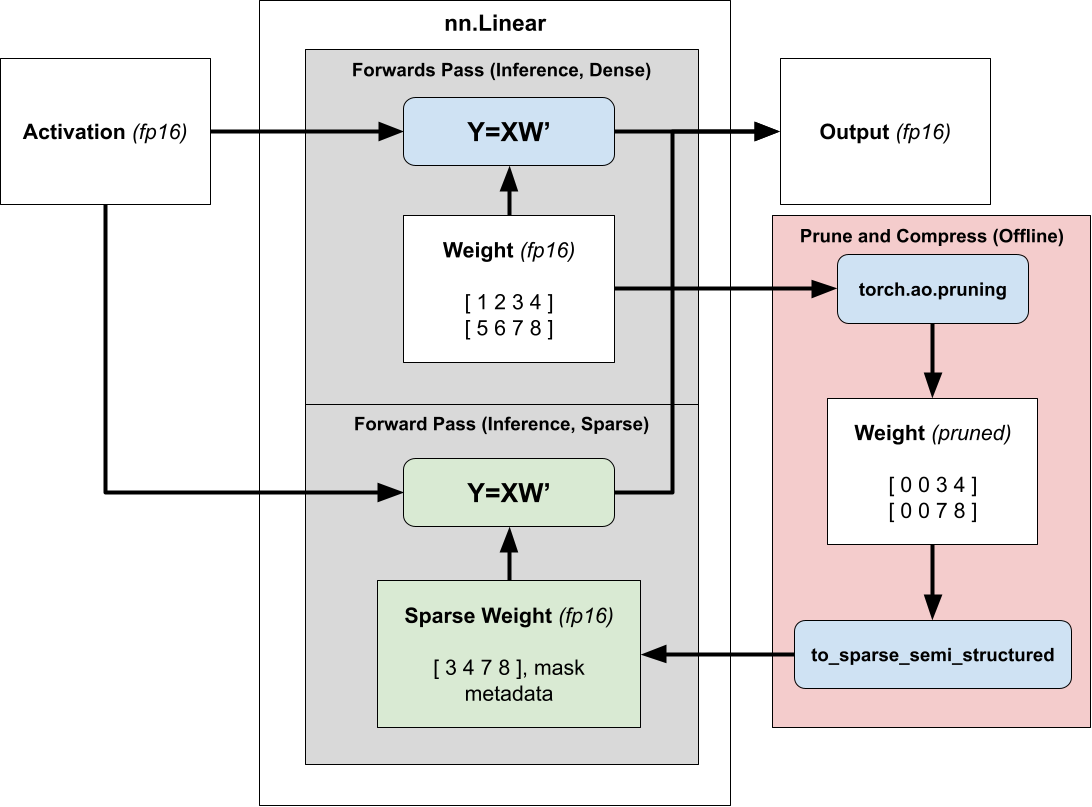
flow chart

然后，我们不再调度密集矩阵乘法，而是调度稀疏矩阵乘法，传入压缩的稀疏权重而不是正常的密集权重。有关使用 2:4 稀疏性加速模型推理的更多信息，请参阅我们的 教程。

将稀疏推理加速扩展到训练

为了利用稀疏性来减少模型的训练时间，我们需要考虑何时计算掩码，因为一旦我们存储了压缩表示，掩码就会固定。

用应用于现有训练好的密集模型的固定掩码进行训练（也称为**修剪**）不会降低准确性，但这需要两次训练运行——一次用于获取密集模型，另一次用于使其稀疏，这样并不能提供加速。

相反，我们希望从头开始训练稀疏模型（**动态稀疏训练**），但从头开始使用固定掩码进行训练会导致评估显著下降，因为稀疏性掩码将在初始化时选择，此时模型权重本质上是随机的。

为了在从头开始训练时保持模型的准确性，我们在运行时修剪和压缩权重，以便我们可以在训练过程的每个步骤计算最优掩码。

从概念上讲，你可以将我们的方法视为一种近似矩阵乘法技术，我们 `prune_and_compress` 并分派到 `sparse_GEMM` 所需的时间少于 `dense_GEMM` 调用所需的时间。这很困难，因为原生修剪和压缩函数太慢，无法显示出加速效果。

鉴于我们 ViT-L 训练矩阵乘法的形状（13008x4096x1024），我们测量了密集 GEMM 和稀疏 GEMM 的运行时间分别为 538us 和 387us。换句话说，权重矩阵的修剪和压缩步骤必须在小于 538-387=151us 的时间内运行才能获得任何效率增益。不幸的是，cuSPARSELt 中提供的压缩内核已经需要 380us（甚至没有考虑修剪步骤！）。

考虑到 NVIDIA A100 的最大内存 IO（2TB/s），并且考虑到修剪和压缩内核会受内存限制，我们理论上可以在 4us 内（8MB / 2TB/s！）修剪和压缩我们的权重（4096x1024x2 字节=8MB）！事实上，我们能够编写一个内核，将矩阵修剪并压缩为 2:4 稀疏格式，并在 36 us 内运行（比 cuSPARSELt 中的压缩内核快 10 倍），使整个 GEMM（包括稀疏化）更快。我们的内核已在 PyTorch 中 可用。

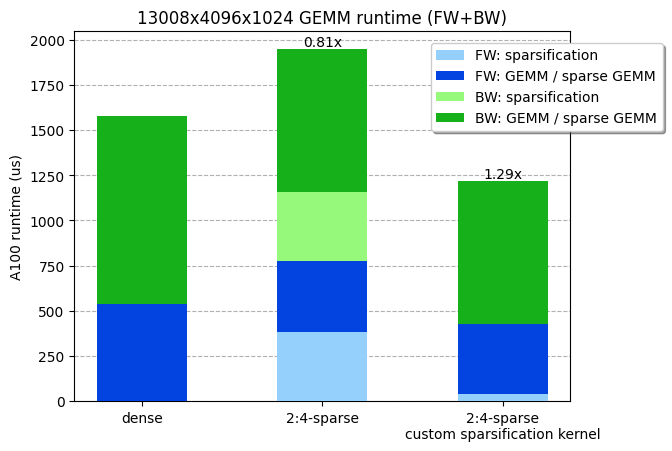
Our custom sparsification kernel

我们定制的稀疏化内核，包括修剪 + 压缩，在线性层前向 + 反向传递中快了约 30%。基准测试在 NVIDIA A100-80GB GPU 上运行。

编写高性能运行时稀疏化内核

为了实现高性能运行时稀疏化内核，我们面临着多项挑战，我们将在下面探讨。

1) 处理反向传播

对于反向传播，我们需要计算 dL/dX 和 dL/dW 以进行梯度更新和后续层，这意味着我们需要分别计算 xWT 和 xTW。

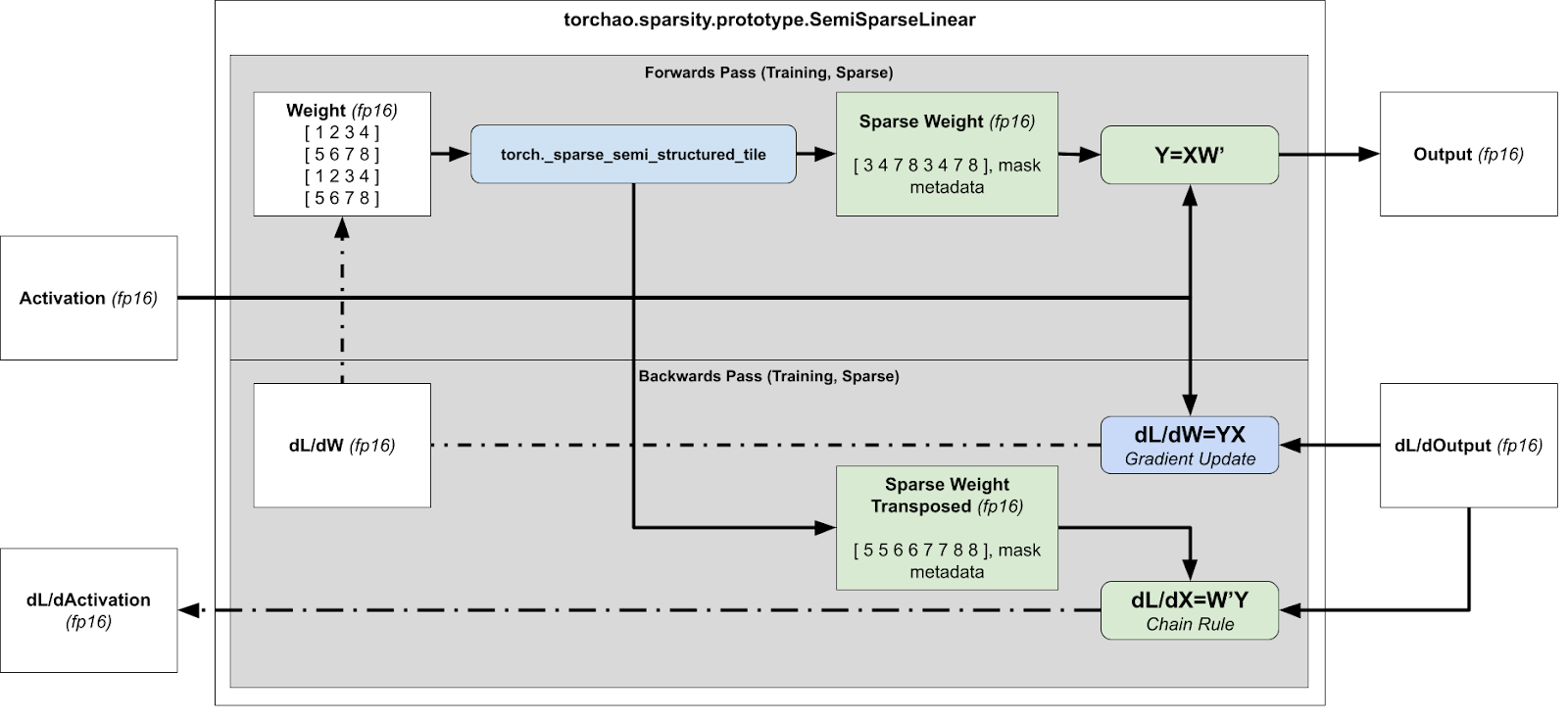
Overview of runtime sparsification for training acceleration (FW + BW pass)

训练加速运行时稀疏化概述（前向 + 反向传播）

然而，这有问题，因为压缩表示无法转置，因为无法保证张量在两个方向上都是 2:4 稀疏的。

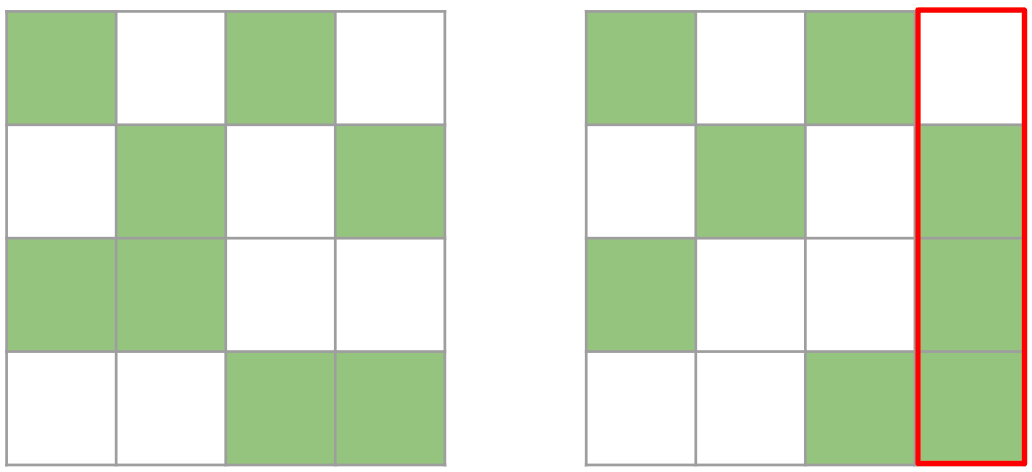
Both matrices are valid 2:4 matrices. However, the right one is no longer a valid 2:4 matrix once transposed because one column contains more than 2 elements

这两个矩阵都是有效的 2:4 矩阵。然而，右边的矩阵在转置后不再是有效的 2:4 矩阵，因为其中一列包含超过 2 个元素。

因此，我们修剪一个 4x4 的块，而不是一个 1x4 的条带。我们贪婪地保留最大值，确保每行/每列最多保留 2 个值。虽然这种方法不能保证最优（因为我们有时只保留 7 个值而不是 8 个），但它能有效地计算出一个在行方向和列方向上都是 2:4 稀疏的张量。

然后，我们同时压缩打包张量和打包转置张量，并存储转置张量用于反向传播。通过同时计算打包张量和打包转置张量，我们避免了在反向传播中的二次内核调用。

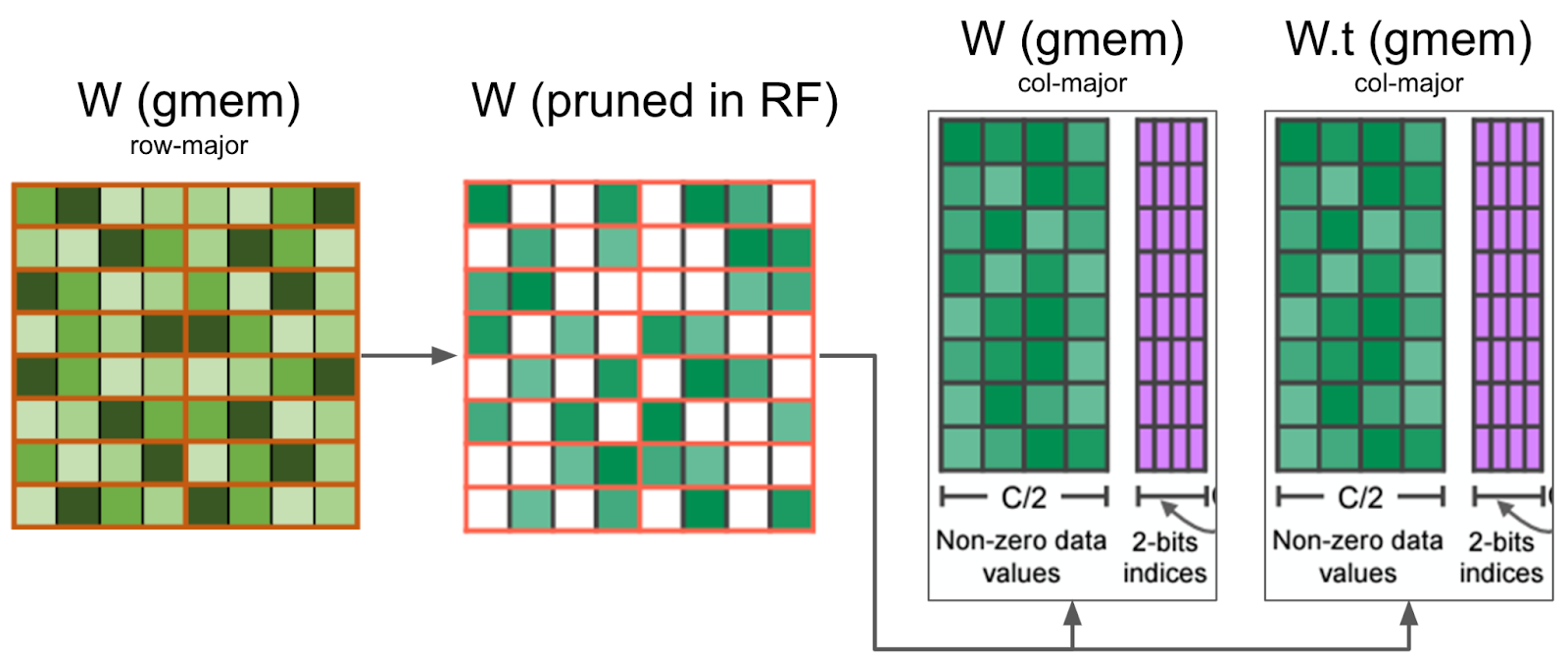
Our kernel prunes the weight matrix in registers

我们的内核在寄存器中修剪权重矩阵，并将压缩值写入全局内存。它还同时修剪了反向传播所需的 W.t，从而最大限度地减少了内存 IO。

为了处理反向传播，还需要一些额外的转置技巧——底层硬件只支持第一个矩阵是稀疏的操作。对于推理期间的权重稀疏化，当我们计算 xWT 时，我们依赖转置属性来交换操作数的顺序。

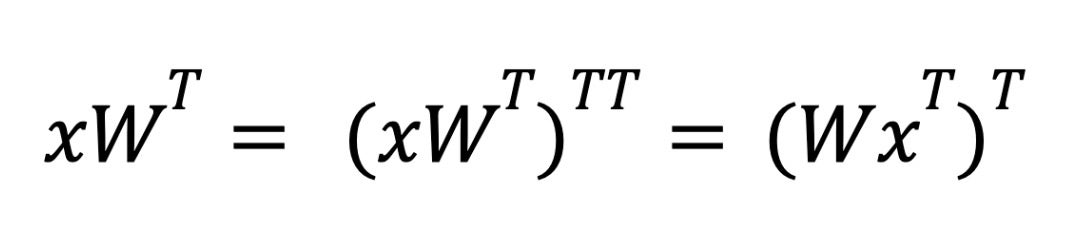
Math formula

在推理过程中，我们使用 `torch.compile` 将外部转置融合到后续的逐点操作中，以避免性能损失。

然而，在训练的反向传播情况下，我们没有后续的逐点操作可以融合。相反，我们通过利用 cuSPARSELt 指定结果矩阵的行/列布局的能力，将转置融合到我们的矩阵乘法中。

2) 高效内存 IO 的内核分块

为了使我们的内核尽可能高效，我们希望合并我们的读/写操作，因为我们发现内存 IO 是主要的瓶颈。这意味着在一个 CUDA 线程中，我们希望一次读/写 128 字节的块，这样多个并行读/写可以被 GPU 内存控制器合并为一个请求。

因此，我们决定每个线程将处理 4 个 4x4 瓦片（即一个 8x8 瓦片），而不是一个线程处理单个 4x4 瓦片（只有 4x4x2 = 32 字节），这使我们能够操作 8x8x2 = 128 字节的块。

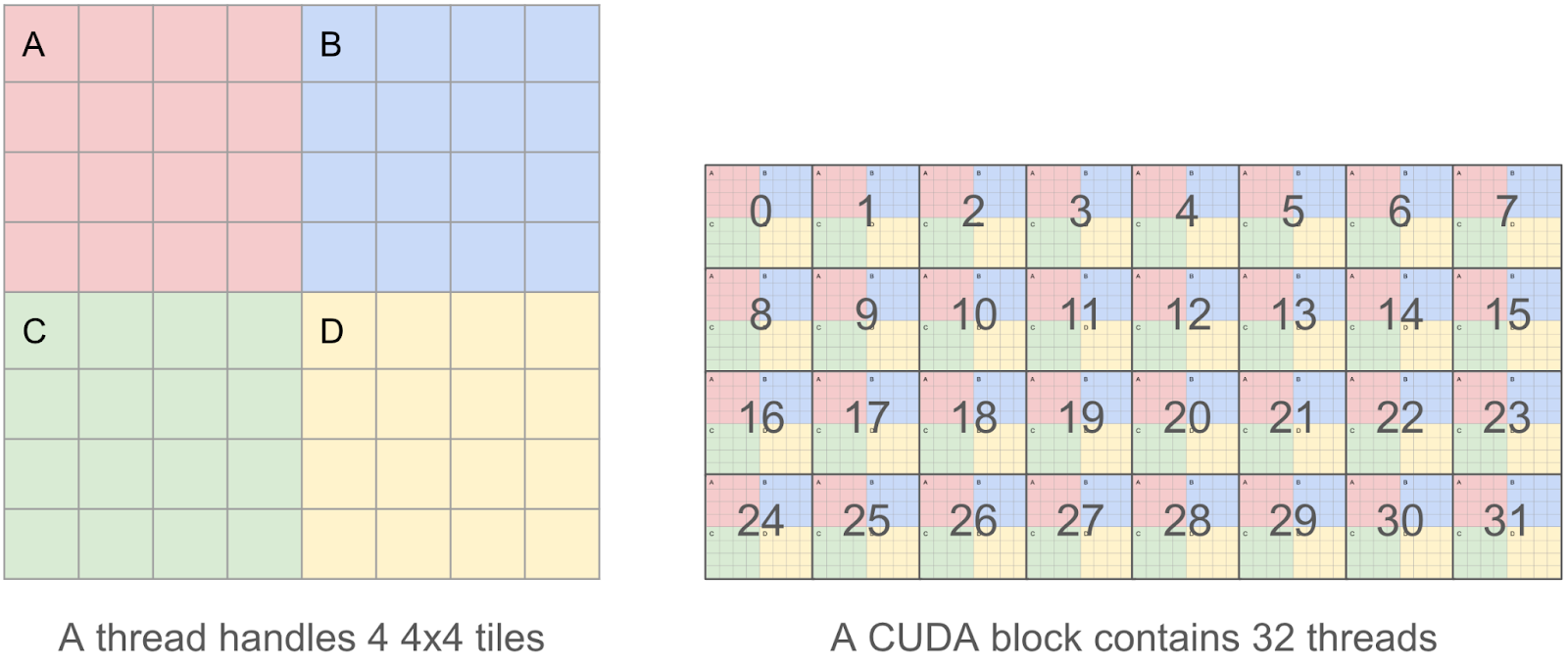
Kernel tiling for efficient memory-IO

3) 在 4x4 瓦片中对元素进行排序而不产生线程束分化

对于线程中的每个 4x4 瓦片，我们计算一个位掩码，指定要修剪哪些元素以及要保留哪些元素。为此，我们对所有 16 个元素进行排序并贪婪地保留元素，只要它们不违反我们的 2:4 行/列约束。这只保留了值最大的权重。

关键是，我们观察到我们只对固定数量的元素进行排序，因此通过使用无分支的 排序网络，我们可以避免线程束分化。

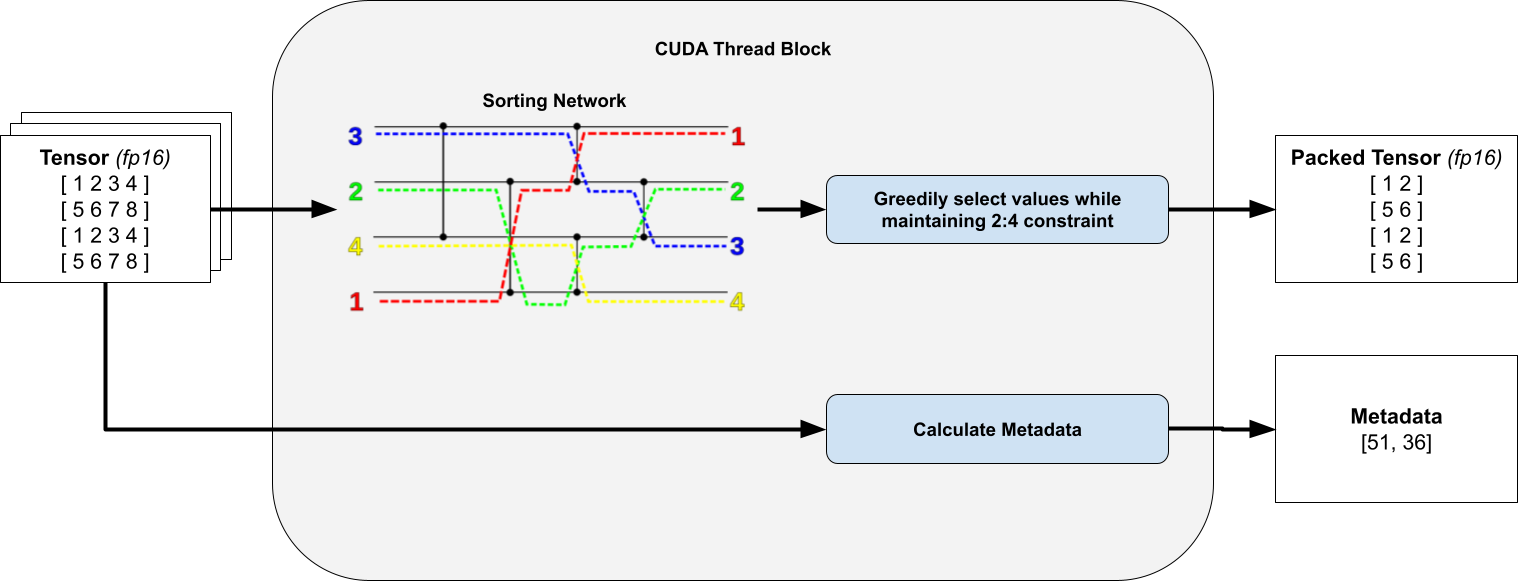
Sorting network diagram

为清晰起见，省略了转置打包张量和元数据。排序网络图取自 Wikipedia。

当我们在线程块中进行条件执行时，会发生线程束分化。在 CUDA 中，同一工作组（线程块）中的工作项在硬件级别以批次（线程束）分派。如果存在条件执行，使得同一批次中的某些工作项运行不同的指令，那么当线程束被分派时，它们会被屏蔽，或者按顺序分派。

例如，如果我们的代码是 `if (condition) do(A) else do(B)`，其中所有奇数工作项都满足 condition，那么此条件语句的总运行时间是 `do(A) + do(B)`，因为我们会为所有奇数工作项分派 `do(A)`，屏蔽偶数工作项，并为所有偶数工作项分派 `do(B)`，屏蔽奇数工作项。此 答案 提供了有关线程束分化的更多信息。

4) 写入压缩矩阵和元数据

一旦位掩码计算完毕，权重数据必须以压缩格式写回全局内存。这并非易事，因为数据需要保留在寄存器中，并且无法索引寄存器（例如 `C[i++] = a` 会阻止我们将 `C` 存储在寄存器中）。此外，我们发现 `nvcc` 使用的寄存器比我们预期的要多得多，这导致寄存器溢出并影响了整体性能。我们将此压缩矩阵以列主序格式写入全局内存，以提高写入效率。

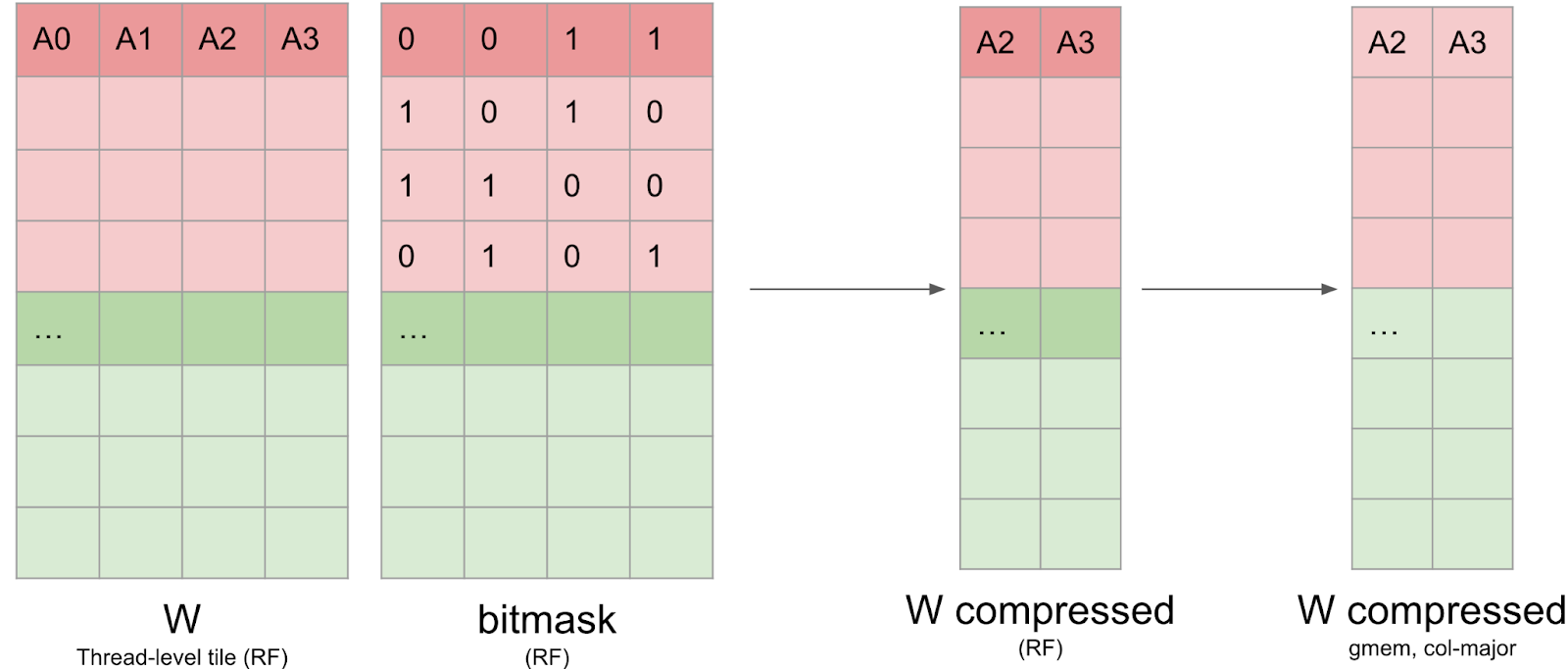
compressed matrix to global memory in Column-Major format

我们还需要写入 cuSPARSELt 元数据。此元数据布局与开源 CUTLASS 库的布局非常相似，并且经过优化，可以通过 PTX `ldmatrix` 指令在 GEMM 内核中高效加载共享内存。

然而，此布局并未优化以高效写入：元数据张量的前 128 位包含有关第 0、8、16 和 24 行的前 32 列的元数据。回想一下，每个线程处理一个 8x8 瓦片，这意味着此信息分散在 16 个线程中。

我们依赖一系列线程束混洗操作，分别用于原始表示和转置表示以写入元数据。幸运的是，此数据仅占总 IO 的不到 10%，因此我们可以承受不完全合并写入的代价。

DINOv2 稀疏训练：实验设置与结果

在我们的实验中，ViT-L 模型使用 DINOv2 方法在 ImageNet 上训练了 125k 步。我们所有的实验都在 4 个 AMD EPYC 7742 64 核 CPU 和 4 个 NVIDIA A100-80GB GPU 上运行。在稀疏训练期间，模型在前一部分训练中启用了 2:4 稀疏性，其中只有一半的权重被启用。权重的稀疏掩码在训练过程的每一步都会动态重新计算，因为权重在优化过程中会不断更新。在剩余的步骤中，模型进行密集训练，生成一个最终没有 2:4 稀疏性的模型（除了 100% 稀疏训练设置），然后进行评估。

训练设置ImageNet 1k 对数回归
0% 稀疏（125k 密集步，基线）82.8
40% 稀疏（50k 稀疏 -> 75k 密集步）82.9
60% 稀疏（75k 稀疏 -> 50k 密集步）82.8
70% 稀疏（87.5k 稀疏 -> 37.5k 密集步）82.7
80% 稀疏（100k 稀疏 -> 25k 密集步）82.7
90% 稀疏（112.5k 稀疏 -> 12.5k 密集步）82.0
100% 稀疏（125k 稀疏步）82.3（2:4 稀疏模型）
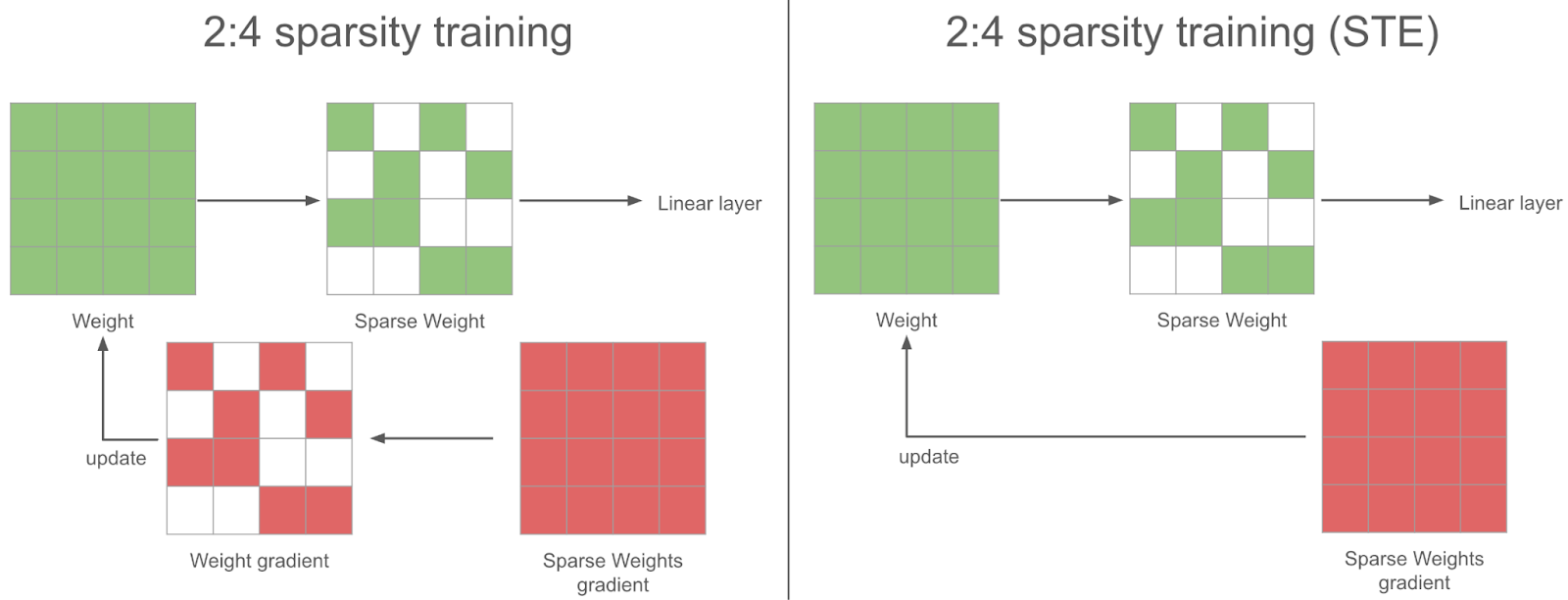
sparsity training diagrams

在稀疏训练步骤中，在反向传播过程中，我们获得了稀疏权重的密集梯度。为了使梯度下降合理，我们也应该在将其用于优化器更新权重之前稀疏化此梯度。相反，我们使用完整的密集梯度来更新权重——我们发现这在实践中效果更好：这就是 STE（Straight Through Estimator）策略。换句话说，我们每一步都会更新所有参数，即使是我们不使用的参数。

结论与未来工作

在这篇博客文章中，我们展示了如何利用半结构化稀疏性加速神经网络训练，并解释了我们面临的一些挑战。我们成功地在 DINOv2 训练中实现了 6% 的端到端加速，且准确率仅下降了 0.1 个百分点。

这项工作有几个扩展领域：

  • **扩展到新的稀疏模式：** 研究人员已经创建了新的稀疏模式，如 V:N:M 稀疏性，它们使用底层半结构化稀疏内核来实现更大的灵活性。这对于将稀疏性应用于大型语言模型（LLM）尤其有趣，因为 2:4 稀疏性会导致准确性下降过多，但我们已经看到了更一般的 N:M 模式的积极 结果。
  • **稀疏微调的性能优化：** 这篇文章涵盖了从头开始的稀疏训练，但通常我们希望微调一个基础模型。在这种情况下，静态掩码可能足以保持准确性，这将使我们能够进行额外的性能优化。
  • **更多关于剪枝策略的实验：** 我们在网络的每一步计算掩码，但每 n 步计算一次掩码可能会产生更好的训练准确性。总的来说，找出在训练过程中使用半结构化稀疏性的最佳策略是一个开放的研究领域。
  • **与 fp8 的兼容性：** 硬件也支持 fp8 半结构化稀疏性，原则上这种方法应该与 fp8 类似地工作。实际上，我们需要编写类似的稀疏化内核，并可能将其与张量缩放融合。
  • **激活稀疏性：** 高效的稀疏化内核还可以在训练期间稀疏化激活。由于稀疏化开销随稀疏矩阵大小线性增长，因此与权重张量相比，具有大激活张量的设置可以从激活稀疏性中获得比权重稀疏性更多的益处。此外，由于使用了 ReLU 或 GELU 激活函数，激活天然是稀疏的，从而减少了准确性下降。

如果您对这些问题感兴趣，请随时在 torchao 中提出问题/PR，这是一个我们正在为量化和稀疏性等架构优化技术构建的社区。此外，如果您对稀疏性普遍感兴趣，请在 CUDA-MODE (#sparsity) 中联系我们。